1 Cover
2 Title Page Finite Element Analysis Method, Verification and Validation Second Edition Barna Szabó Washington University in St. Louis Ivo Babuška The University of Texas at Austin
3 Copyright
4 Preface to the second edition
5 Preface to the first edition Notes
6 Preface
7 About the companion website
8 1 Introduction to the finite element method 1.1 An introductory problem 1.2 Generalized formulation 1.3 Approximate solutions 1.4 Post‐solution operations 1.5 Estimation of error in energy norm 1.6 The choice of discretization in 1D 1.7 Eigenvalue problems 1.8 Other finite element methods Notes
9 2 Boundary value problems 2.1 Notation 2.2 The scalar elliptic boundary value problem 2.3 Heat conduction 2.4 Equations of linear elasticity – strong form 2.5 Stokes flow 2.6 Generalized formulation of problems of linear elasticity 2.7 Residual stresses 2.8 Chapter summary Notes
10 3 Implementation 3.1 Standard elements in two dimensions 3.2 Standard polynomial spaces 3.3 Shape functions 3.4 Mapping functions in two dimensions 3.5 Finite element spaces in two dimensions 3.6 Essential boundary conditions 3.7 Elements in three dimensions 3.8 Integration and differentiation 3.9 Stiffness matrices and load vectors 3.10 Post‐solution operations 3.11 Computation of the solution and its first derivatives 3.12 Nodal forces 3.13 Chapter summary Notes
11 4 Pre‐ and postprocessing procedures and verification 4.1 Regularity in two and three dimensions 4.2 The Laplace equation in two dimensions 4.3 The Laplace equation in three dimensions 4.4 Planar elasticity 4.5 Robustness 4.6 Solution verification Notes
12 5 Simulation 5.1 Development of a very useful mathematical model 5.2 Finite element modeling and numerical simulation Notes
13 6 Calibration, validation and ranking 6.1 Fatigue data 6.2 The predictors of Peterson and Neuber 6.3 The predictor Gα 6.4 Biaxial test data 6.5 Management of model development Notes
14 7 Beams, plates and shells 7.1 Beams 7.2 Plates 7.3 Shells 7.4 Chapter summary Notes
15 8 Aspects of multiscale models 8.1 Unidirectional fiber‐reinforced laminae 8.2 Discussion Notes
16 9 Non‐linear models 9.1 Heat conduction 9.2 Solid mechanics 9.3 Chapter summary Notes
17 Appendix A: Appendix ADefinitionsDefinitions A.1 Normed linear spaces, linear functionals and bilinear forms A.2 Convergence in the space A.3 The Schwarz inequality for integrals Notes
18 Appendix B: Appendix BProof of h‐convergenceProof of h‐convergence
19 Appendix C: Appendix CConvergence in 3D: Empirical resultsConvergence in 3D: Empirical results
20 Appendix D: Appendix DLegendre polynomialsLegendre polynomials D.1 Shape functions based on Legendre polynomials
21 Appendix E: Appendix ENumerical quadratureNumerical quadrature E.1 Gaussian quadrature E.2 Gauss‐Lobatto quadrature Note
22 Appendix F: Appendix FPolynomial mapping functionsPolynomial mapping functions F.1 Interpolation on surfaces
23 Appendix G: Appendix GCorner singularities in two‐dimensional elasticityCorner singularities in two‐dimensional elasticity G.1 The Airy stress function G.2 Stress‐free edges Notes
24 Appendix H: Appendix HComputation of stress intensity factorsComputation of stress intensity factors H.1 Singularities at crack tips H.2 The contour integral method H.3 The energy release rate Note
25 Appendix I: Appendix IFundamentals of data analysisFundamentals of data analysis I.1 Statistical foundations I.2 Test data I.3 Statistical models I.4 Ranking I.5 Confidence intervals Notes
26 Appendix J: Appendix JEstimation of fastener forces in structural connectionsEstimation of fastener forces in structural connections
27 Appendix K: Appendix KUseful algorithms in solid mechanicsUseful algorithms in solid mechanics K.1 The traction vector K.2 Transformation of vectors K.3 Transformation of stresses K.4 Principal stresses K.5 The von Mises stress K.6 Statically equivalent forces and moments Notes
28 Bibliography
29 Index
30 End User License Agreement
1 Chapter 1 Table 1.1 Local and global numbering in Example 1.6. Table 1.2 Exact values of the potential energy for 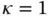 ,
, 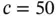 and
and 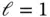 . Table 1.3 Example: Computed and estimated values of the potential energy
. Table 1.3 Example: Computed and estimated values of the potential energy 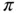 . Un... Table 1.4 Example: Element‐by‐element and total relative errors in energy nor... Table 1.5 Example: Element‐by‐element and total relative errors in energy nor... Table 1.6 Example: p ‐Convergence of the 24th eigenvalue in Example 1.16. Table 1.7 The computed values of
. Un... Table 1.4 Example: Element‐by‐element and total relative errors in energy nor... Table 1.5 Example: Element‐by‐element and total relative errors in energy nor... Table 1.6 Example: p ‐Convergence of the 24th eigenvalue in Example 1.16. Table 1.7 The computed values of 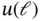 .
.
2 Chapter 2Table 2.1 Exercise 2.30: Boundary conditions
3 Chapter 3Table 3.1 Example 3.3. Nodal forces (kN). The notation is shown in Fig. 3.12(...Table 3.2 Example 3.3. Nodal forces (kN). Solution on the shaded domain shown...
4 Chapter 4Table 4.1 L‐shaped domain, radical mesh ( 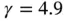 ), 27 elements, product space. Esti...Table 4.2 L‐shaped domain, radical mesh (
), 27 elements, product space. Esti...Table 4.2 L‐shaped domain, radical mesh ( 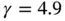 ), 27 elements, product space. Esti...Table 4.3 Example 4.1: The results of extraction by the contour integral meth...Table 4.4 The Fichera domain. p ‐convergence, radical mesh
), 27 elements, product space. Esti...Table 4.3 Example 4.1: The results of extraction by the contour integral meth...Table 4.4 The Fichera domain. p ‐convergence, radical mesh 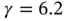 ,
, 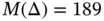 , product space....Table 4.5 Fichera domain. h ‐convergence, uniform mesh refinement,
, product space....Table 4.5 Fichera domain. h ‐convergence, uniform mesh refinement, 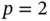 (product s...Table 4.6 The Fichera domain. p ‐convergence, uniform mesh,
(product s...Table 4.6 The Fichera domain. p ‐convergence, uniform mesh, 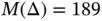 , product space.Table 4.7 L‐shaped domain, free‐free boundary conditions, plane strain,
, product space.Table 4.7 L‐shaped domain, free‐free boundary conditions, plane strain, 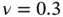 , rad...Table 4.8 Convergence of the strain energy (
, rad...Table 4.8 Convergence of the strain energy ( 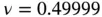 ). Rigid circular inclusion in a...Table 4.9 Example 4.6. Rigid circular inclusion in an infinite plate under te...Table 4.10 Example 4.7: Estimated error in energy norm.Table 4.11 Geometric and material properties.
). Rigid circular inclusion in a...Table 4.9 Example 4.6. Rigid circular inclusion in an infinite plate under te...Table 4.10 Example 4.7: Estimated error in energy norm.Table 4.11 Geometric and material properties.
5 Chapter 5Table 5.1 Legacy codes: Summary of results.Table 5.2 Numerical simulation codes: Summary of results.Table 5.3 Solution by classical methods: Summary of results.Table 5.4 Fastener forces estimated by the method described in Appendix JTable 5.5 Fastener forces estimated by the linear spring modelTable 5.6 Fastener forces estimated by the nonlinear spring modelTable 5.7 Fastener forces estimated by the multibody contact modelTable 5.8 Example 5.1. Fastener forces estimated by the nonlinear spring mode...Table 5.9 Fastener forces estimated by finite element modelingTable 5.10 Quantities of interest from finite element modeling and Model 3 (k...Table 5.11 Linear model. Computed values of the strain energy ( 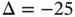 mm).Table 5.12 Linear model. Computed stress resultants in the local coordinate s...Table 5.13 Nonlinear model,
mm).Table 5.12 Linear model. Computed stress resultants in the local coordinate s...Table 5.13 Nonlinear model, 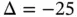 mm. Computed stress resultants in the global coo...Table 5.14 Linear model of the coil segment. Computed values of the strain en...
mm. Computed stress resultants in the global coo...Table 5.14 Linear model of the coil segment. Computed values of the strain en...
Читать дальше

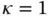 ,
, 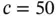 and
and 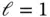 . Table 1.3 Example: Computed and estimated values of the potential energy
. Table 1.3 Example: Computed and estimated values of the potential energy 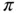 . Un... Table 1.4 Example: Element‐by‐element and total relative errors in energy nor... Table 1.5 Example: Element‐by‐element and total relative errors in energy nor... Table 1.6 Example: p ‐Convergence of the 24th eigenvalue in Example 1.16. Table 1.7 The computed values of
. Un... Table 1.4 Example: Element‐by‐element and total relative errors in energy nor... Table 1.5 Example: Element‐by‐element and total relative errors in energy nor... Table 1.6 Example: p ‐Convergence of the 24th eigenvalue in Example 1.16. Table 1.7 The computed values of 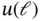 .
.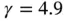 ), 27 elements, product space. Esti...Table 4.2 L‐shaped domain, radical mesh (
), 27 elements, product space. Esti...Table 4.2 L‐shaped domain, radical mesh ( 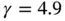 ), 27 elements, product space. Esti...Table 4.3 Example 4.1: The results of extraction by the contour integral meth...Table 4.4 The Fichera domain. p ‐convergence, radical mesh
), 27 elements, product space. Esti...Table 4.3 Example 4.1: The results of extraction by the contour integral meth...Table 4.4 The Fichera domain. p ‐convergence, radical mesh 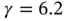 ,
, 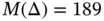 , product space....Table 4.5 Fichera domain. h ‐convergence, uniform mesh refinement,
, product space....Table 4.5 Fichera domain. h ‐convergence, uniform mesh refinement, 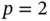 (product s...Table 4.6 The Fichera domain. p ‐convergence, uniform mesh,
(product s...Table 4.6 The Fichera domain. p ‐convergence, uniform mesh, 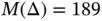 , product space.Table 4.7 L‐shaped domain, free‐free boundary conditions, plane strain,
, product space.Table 4.7 L‐shaped domain, free‐free boundary conditions, plane strain, 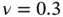 , rad...Table 4.8 Convergence of the strain energy (
, rad...Table 4.8 Convergence of the strain energy ( 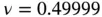 ). Rigid circular inclusion in a...Table 4.9 Example 4.6. Rigid circular inclusion in an infinite plate under te...Table 4.10 Example 4.7: Estimated error in energy norm.Table 4.11 Geometric and material properties.
). Rigid circular inclusion in a...Table 4.9 Example 4.6. Rigid circular inclusion in an infinite plate under te...Table 4.10 Example 4.7: Estimated error in energy norm.Table 4.11 Geometric and material properties.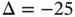 mm).Table 5.12 Linear model. Computed stress resultants in the local coordinate s...Table 5.13 Nonlinear model,
mm).Table 5.12 Linear model. Computed stress resultants in the local coordinate s...Table 5.13 Nonlinear model, 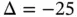 mm. Computed stress resultants in the global coo...Table 5.14 Linear model of the coil segment. Computed values of the strain en...
mm. Computed stress resultants in the global coo...Table 5.14 Linear model of the coil segment. Computed values of the strain en...










