(1.173) 
Table 1.7 The computed values of 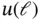 .
.
| γ |
10 −3 |
10 −6 |
10 −9 |
10 −12 |
10 −15 |
| u ( ℓ ) |
0.2540348 |
0.2500004 |
0.25(0) 64 |
0.25(0) 94 |
0.25(0) 124 |
where p is the polynomial degree. Therefore 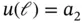 and
and 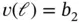 and, using the Legendre shape functions, for
and, using the Legendre shape functions, for 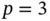 the unconstrained coefficient matrix, without the modifications of Nitsche, is
the unconstrained coefficient matrix, without the modifications of Nitsche, is
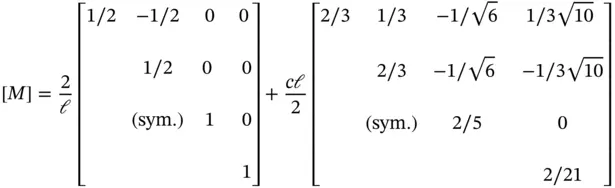
Referring to eq. (1.172), the coefficient matrix is modified by the application of Nitsche's method. Those modifications in the present case are:
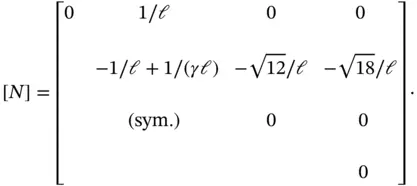
The unconstrained right hand side vector without the modifications of Nitsche is:
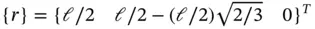
and with the modifications of Nitsche it is:
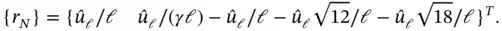
The numerical results shown in Table 1.7indicate that the stabilized formulation is remarkably robust. The notation 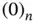 indicates that there are n zeros.
indicates that there are n zeros.
1 1Ludwig Prandtl 1875–1953.
2 2The generalized form is also called variational form or weak form.
3 3The term “discretization” refers to processes by which approximating functions are defined. The most widely used discretizations will be described and illustrated by examples in this and subsequent chapters.
4 4See Definition A.5 in the appendix.
5 5Peter Gustav Lejeune Dirichlet 1805–1859.
6 6Carl Gottfried Neumann 1832–1925.
7 7Victor Gustave Robin (1855–1897).
8 8A functional is a real‐valued function defined on a space of functions or vectors.
9 9Leonhard Euler 1707–1783.
10 10Joseph‐Louis Lagrange 1736–1813.
11 11Boris Grigoryevich Galerkin 1871–1945.
12 12Adrien‐Marie Legendre 1752–1833.
13 13Jörgen Pedersen Gram 1850–1916.
14 14The definition of is given by eq. (2.1).
15 15John William Strutt, 3rd Baron Rayleigh 1842–1919.
16 16Joachim Nitsche 1926–1996.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.


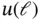 .
.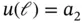 and
and 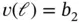 and, using the Legendre shape functions, for
and, using the Legendre shape functions, for 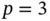 the unconstrained coefficient matrix, without the modifications of Nitsche, is
the unconstrained coefficient matrix, without the modifications of Nitsche, is
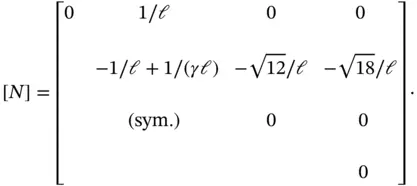
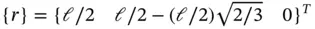
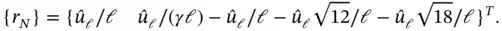
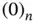 indicates that there are n zeros.
indicates that there are n zeros.










