|
Element number |
|
| α |
1 |
2 |
3 |
4 |
5 |
 |
| 1 |
0 |
0 |
0 |
0 |
0 |
0 |
| 2 |
11.00 |
61.24 |
15.31 |
7.02 |
4.55 |
2.45 |
| 3 |
20.09 |
4.69 |
98.83 |
16.16 |
9.24 |
4.62 |
| 4 |
36.98 |
8.41 |
17.24 |
30.13 |
14.02 |
8.00 |
Errors in numerical integration can be particularly damaging. The reader should be mindful of this when applying the concepts and procedures discussed in this chapter to higher dimensions.
The following problem is a prototype of an important class of engineering problems which includes the undamped vibration of elastic structures:
(1.133) 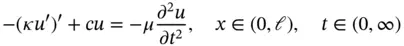
where the primes represent differentiation with respect to x . For example, we may think of an elastic bar of length 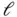 , cross‐section A , modulus of elasticity E , in which case
, cross‐section A , modulus of elasticity E , in which case 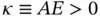 given in units of Newton (N) or equivalent, the parameter
given in units of Newton (N) or equivalent, the parameter 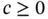 is the coefficient of distributed springs (
is the coefficient of distributed springs ( 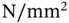 ) and the parameter
) and the parameter 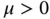 is mass per unit length (kg/m =
is mass per unit length (kg/m = 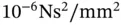 ). The bar is vibrating in its longitudinal direction.
). The bar is vibrating in its longitudinal direction.
The boundary conditions are:

and the initial conditions are
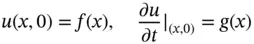
where 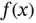 and
and 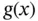 are given functions in
are given functions in 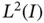 . Here we consider homogeneous Dirichlet boundary conditions. However, the boundary conditions can be homogeneous Neumann or homogeneous Robin conditions, or any combination of those.
. Here we consider homogeneous Dirichlet boundary conditions. However, the boundary conditions can be homogeneous Neumann or homogeneous Robin conditions, or any combination of those.
The generalized form is obtained by multiplying eq. (1.133)by a test function 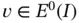 and integrating by parts:
and integrating by parts:
(1.134) 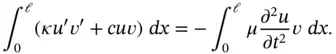
We now introduce 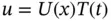 where
where 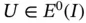 ,
, 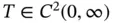 . This is known as separation of variables. Therefore we get
. This is known as separation of variables. Therefore we get
(1.135) 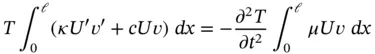
which can be written as
(1.136) 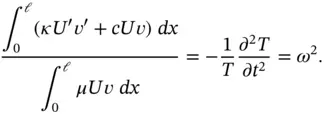
Since the functions on the left are independent of t , the function T depends only on t , both expressions must equal some positive constant denoted by 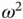 . That constant has to be positive because the expression on the left holds for all
. That constant has to be positive because the expression on the left holds for all 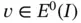 and if we select
and if we select 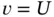 then the expression on the left is positive.
then the expression on the left is positive.
The function 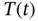 satisfies the ordinary differential equation
satisfies the ordinary differential equation
(1.137) 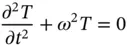
the solution of which is
(1.138) 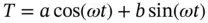
where ω is the angular velocity (rad/s). Alternatively ω is written as 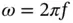 where f is the frequency (Hz).
where f is the frequency (Hz).
To find ω and U we have to solve the problem
(1.139) 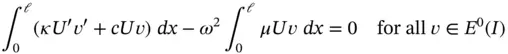
which will be abbreviated as
(1.140) 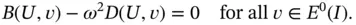
There are infinitely many solutions called eigenpairs 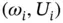 ,
, 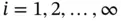 . The set of eigenvalues is called the spectrum. If Ui is an eigenfunction and α is a real number then
. The set of eigenvalues is called the spectrum. If Ui is an eigenfunction and α is a real number then 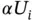 is also an eigenfunction. In the following we assume that the eigenfunctions have been normalized so that
is also an eigenfunction. In the following we assume that the eigenfunctions have been normalized so that
Читать дальше

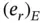
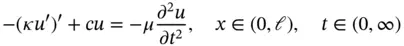
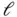 , cross‐section A , modulus of elasticity E , in which case
, cross‐section A , modulus of elasticity E , in which case 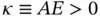 given in units of Newton (N) or equivalent, the parameter
given in units of Newton (N) or equivalent, the parameter 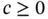 is the coefficient of distributed springs (
is the coefficient of distributed springs ( 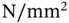 ) and the parameter
) and the parameter 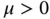 is mass per unit length (kg/m =
is mass per unit length (kg/m = 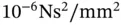 ). The bar is vibrating in its longitudinal direction.
). The bar is vibrating in its longitudinal direction.
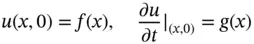
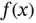 and
and 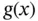 are given functions in
are given functions in 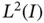 . Here we consider homogeneous Dirichlet boundary conditions. However, the boundary conditions can be homogeneous Neumann or homogeneous Robin conditions, or any combination of those.
. Here we consider homogeneous Dirichlet boundary conditions. However, the boundary conditions can be homogeneous Neumann or homogeneous Robin conditions, or any combination of those.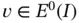 and integrating by parts:
and integrating by parts: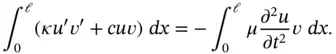
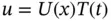 where
where 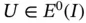 ,
, 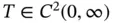 . This is known as separation of variables. Therefore we get
. This is known as separation of variables. Therefore we get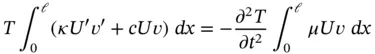
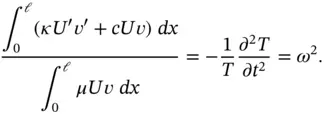
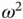 . That constant has to be positive because the expression on the left holds for all
. That constant has to be positive because the expression on the left holds for all  and if we select
and if we select 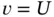 then the expression on the left is positive.
then the expression on the left is positive.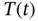 satisfies the ordinary differential equation
satisfies the ordinary differential equation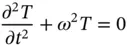
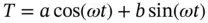
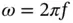 where f is the frequency (Hz).
where f is the frequency (Hz).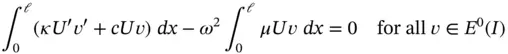
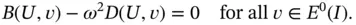
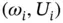 ,
, 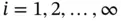 . The set of eigenvalues is called the spectrum. If Ui is an eigenfunction and α is a real number then
. The set of eigenvalues is called the spectrum. If Ui is an eigenfunction and α is a real number then 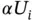 is also an eigenfunction. In the following we assume that the eigenfunctions have been normalized so that
is also an eigenfunction. In the following we assume that the eigenfunctions have been normalized so that










