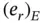The solution is
(1.125) 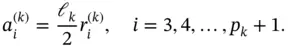
Using eq. (1.106)we get
(1.126) 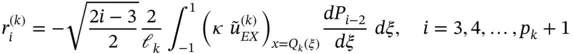
where 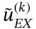 is the difference between
is the difference between 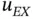 and its linear interpolant:
and its linear interpolant:
(1.127) 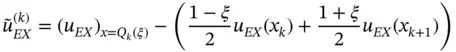
and compute
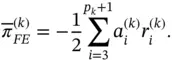
Referring to Theorem 1.5, the error in energy norm associated with the k th element is
(1.128) 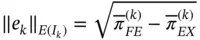
and the relative error in energy norm associated with the k th element is:
(1.129) 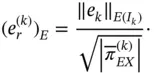
The error of approximation over the entire domain is:
(1.130) 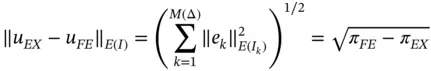
By Theorem 1.2, the exact value of the potential energy is
(1.131) 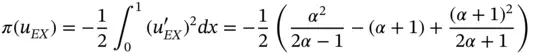
and the relative error in energy norm on the entire domain is:
(1.132) 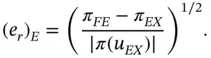
Remark 1.13In estimating the local error we used 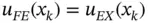 . It can be shown that in the special case of this problem (
. It can be shown that in the special case of this problem ( 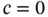 ) this relationship holds and therefore using the equal sign in eq. (1.128)is justified. In the general case (
) this relationship holds and therefore using the equal sign in eq. (1.128)is justified. In the general case ( 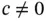 ) however,
) however, 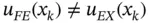 and eq. (1.128)will be an estimate of the local error in the finite element solution. Therefore the equal sign in eq. (1.128)has to be replaced by the approximately equal (
and eq. (1.128)will be an estimate of the local error in the finite element solution. Therefore the equal sign in eq. (1.128)has to be replaced by the approximately equal ( 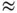 ) sign and the first equal sign in eq. (1.130)has to be replaced with the less or equal (
) sign and the first equal sign in eq. (1.130)has to be replaced with the less or equal ( 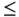 ) sign.
) sign.
Example 1.13This example illustrates the distribution of the relative error among the elements for a fixed mesh and polynomial degree for selected fractional values of α . Uniform mesh on the domain 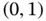 with
with 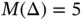 and
and 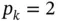 for
for 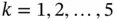 is used. The exact solution for
is used. The exact solution for 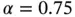 is shown in Fig. 1.12. The percent relative error in energy norm associated with the k th element, given by eq. (1.129), is shown in Table 1.4and the relative error for the entire domain is shown in the last column.
is shown in Fig. 1.12. The percent relative error in energy norm associated with the k th element, given by eq. (1.129), is shown in Table 1.4and the relative error for the entire domain is shown in the last column.
It is seen that for all values of α the maximum error is associated with the first element.
Example 1.14This example illustrates the distribution of the relative error among the elements for a fixed mesh and polynomial degree for selected integer values of α . Uniform mesh on the domain 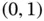 with
with 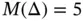 and
and 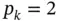 for
for 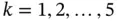 is used. The percent relative error in energy norm associated with the k th element, given by eq. (1.129), is shown in Table 1.5and the relative error for the entire domain is shown in the last column.
is used. The percent relative error in energy norm associated with the k th element, given by eq. (1.129), is shown in Table 1.5and the relative error for the entire domain is shown in the last column.
The error of approximation for 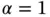 is zero. This follows directly from Theorem 1.4: The exact solution is a polynomial of degree 2. Therefore it lies in the finite element space and hence the finite element solution is the same as the exact solution.
is zero. This follows directly from Theorem 1.4: The exact solution is a polynomial of degree 2. Therefore it lies in the finite element space and hence the finite element solution is the same as the exact solution.
Remark 1.14In the foregoing discussion it was tacitly assumed that all data computed by numerical integration were accurate and the coefficient matrices of the linear equations were such that small changes in the right‐hand‐side vector produce small changes in the solution vector. This happens when the condition number of the coefficient matrix is reasonably small. In the finite element method the condition number depends on the choice of the shape functions, the mapping functions and the mesh. In one‐dimensional setting the mapping is linear and the shape functions are energy‐orthogonal, therefore round‐off errors are not significant. This is not the case in two and three dimensions, however.
Table 1.4 Example: Element‐by‐element and total relative errors in energy norm (percent) for selected fractional values of α .
|
Element number |
|
| α |
1 |
2 |
3 |
4 |
5 |
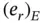 |
| 1.25 |
79.49 |
7.50 |
2.80 |
1.63 |
1.12 |
4.80 |
| 1.15 |
99.52 |
4.06 |
1.63 |
0.97 |
0.67 |
3.92 |
| 1.05 |
29.56 |
1.24 |
0.53 |
0.32 |
0.22 |
1.77 |
| 0.95 |
18.89 |
1.16 |
0.52 |
0.32 |
0.22 |
2.41 |
| 0.85 |
42.94 |
3.26 |
1.52 |
0.94 |
0.67 |
9.84 |
| 0.75 |
60.39 |
5.14 |
2.47 |
1.56 |
1.11 |
22.37 |
| 0.65 |
76.07 |
6.86 |
3.39 |
2.16 |
1.56 |
42.91 |
| 0.55 |
91.80 |
8.44 |
4.28 |
2.76 |
2.00 |
76.22 |
Table 1.5 Example: Element‐by‐element and total relative errors in energy norm (percent) for selected integer values of α .
Читать дальше

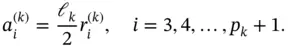
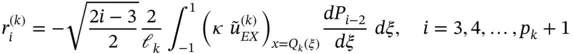
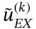 is the difference between
is the difference between 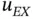 and its linear interpolant:
and its linear interpolant: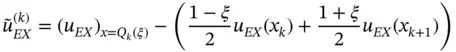
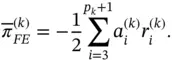
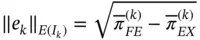
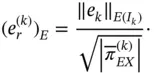
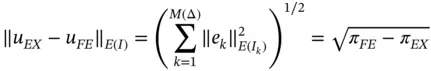
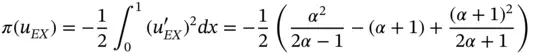
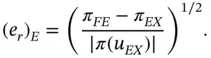
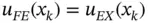 . It can be shown that in the special case of this problem (
. It can be shown that in the special case of this problem ( 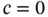 ) this relationship holds and therefore using the equal sign in eq. (1.128)is justified. In the general case (
) this relationship holds and therefore using the equal sign in eq. (1.128)is justified. In the general case ( 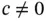 ) however,
) however, 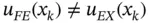 and eq. (1.128)will be an estimate of the local error in the finite element solution. Therefore the equal sign in eq. (1.128)has to be replaced by the approximately equal (
and eq. (1.128)will be an estimate of the local error in the finite element solution. Therefore the equal sign in eq. (1.128)has to be replaced by the approximately equal ( 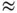 ) sign and the first equal sign in eq. (1.130)has to be replaced with the less or equal (
) sign and the first equal sign in eq. (1.130)has to be replaced with the less or equal ( 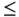 ) sign.
) sign.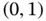 with
with 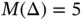 and
and 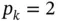 for
for 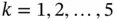 is used. The exact solution for
is used. The exact solution for 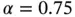 is shown in Fig. 1.12. The percent relative error in energy norm associated with the k th element, given by eq. (1.129), is shown in Table 1.4and the relative error for the entire domain is shown in the last column.
is shown in Fig. 1.12. The percent relative error in energy norm associated with the k th element, given by eq. (1.129), is shown in Table 1.4and the relative error for the entire domain is shown in the last column.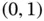 with
with 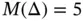 and
and 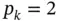 for
for 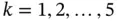 is used. The percent relative error in energy norm associated with the k th element, given by eq. (1.129), is shown in Table 1.5and the relative error for the entire domain is shown in the last column.
is used. The percent relative error in energy norm associated with the k th element, given by eq. (1.129), is shown in Table 1.5and the relative error for the entire domain is shown in the last column.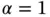 is zero. This follows directly from Theorem 1.4: The exact solution is a polynomial of degree 2. Therefore it lies in the finite element space and hence the finite element solution is the same as the exact solution.
is zero. This follows directly from Theorem 1.4: The exact solution is a polynomial of degree 2. Therefore it lies in the finite element space and hence the finite element solution is the same as the exact solution.