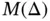 |
N |
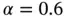 |
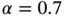 |
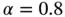 |
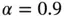 |
| 10 |
19 |
−2.17753673 |
−1.73038992 |
−1.41382648 |
−1.17955239 |
| 100 |
199 |
−2.25079984 |
−1.74673700 |
−1.41675042 |
−1.17984996 |
| 1000 |
1999 |
−2.29589857 |
−1.75303348 |
−1.41745363 |
−1.17989453 |
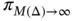 |
−2.37254083 |
−1.75716094 |
−1.41768637 |
−1.17990276 |
the estimated relative error in energy norm for 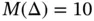 ,
, 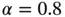 is:
is:
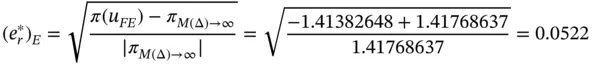
or 5.22%. When using the exact value of the potential energy for reference then the relative error is the same as the estimated relative error to within three digits of accuracy:
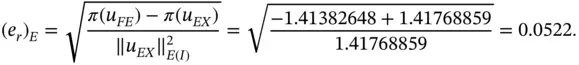
Exercise 1.20Compare the estimated and exact values of the relative error in energy norm for the problem in Example 1.10for 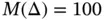 ,
, 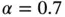 .
.
Example 1.11Let us consider once again model problems in the form of eq. (1.103)with the data: 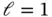 ,
, 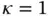 ,
, 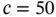 and exact solutions corresponding to
and exact solutions corresponding to 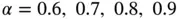 , see eq. (1.104). Using a sequence of uniform finite element meshes with
, see eq. (1.104). Using a sequence of uniform finite element meshes with 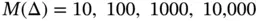 and
and 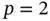 assigned to each element, the results shown in Fig. 1.9are obtained. The values of β were computed by linear regression using eq. (1.101). We observe that
assigned to each element, the results shown in Fig. 1.9are obtained. The values of β were computed by linear regression using eq. (1.101). We observe that 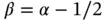 . This is consistent with the asymptotic estimate given by eq. (1.91).
. This is consistent with the asymptotic estimate given by eq. (1.91).
Example 1.12Let us consider model problems in the form of eq. (1.103)with the data: 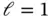 ,
, 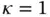 ,
, 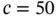 and exact solutions corresponding to
and exact solutions corresponding to 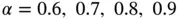 , see eq. (1.104). Using a uniform finite element mesh with
, see eq. (1.104). Using a uniform finite element mesh with 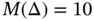 and
and 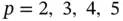 assigned to each element, the results shown in Fig. 1.10are obtained. The values of β were computed by linear regression using eq. (1.101). We observe that
assigned to each element, the results shown in Fig. 1.10are obtained. The values of β were computed by linear regression using eq. (1.101). We observe that 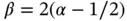 , that is, the rate of convergence is twice that in Example 1.11. This is consistent with the theoretical results in [22, 84]: The rate of p ‐convergence is at least twice the rate of h ‐convergence when the singular point is a nodal point.
, that is, the rate of convergence is twice that in Example 1.11. This is consistent with the theoretical results in [22, 84]: The rate of p ‐convergence is at least twice the rate of h ‐convergence when the singular point is a nodal point.
1.5.4 Error in the extracted QoI
In Example 1.9it was demonstrated that the QoI can be extracted from the finite element solution efficiently and accurately even when the discretization was very poorly chosen. Let us consider a quantity of interest  and the corresponding extraction function
and the corresponding extraction function  . The extracted value of the QoI is
. The extracted value of the QoI is
(1.109) 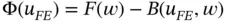
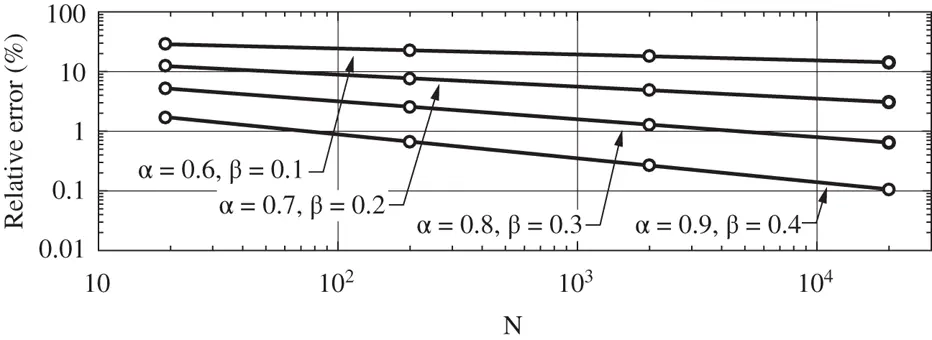
Figure 1.9 Relative error in energy norm.  ,
,  .
.
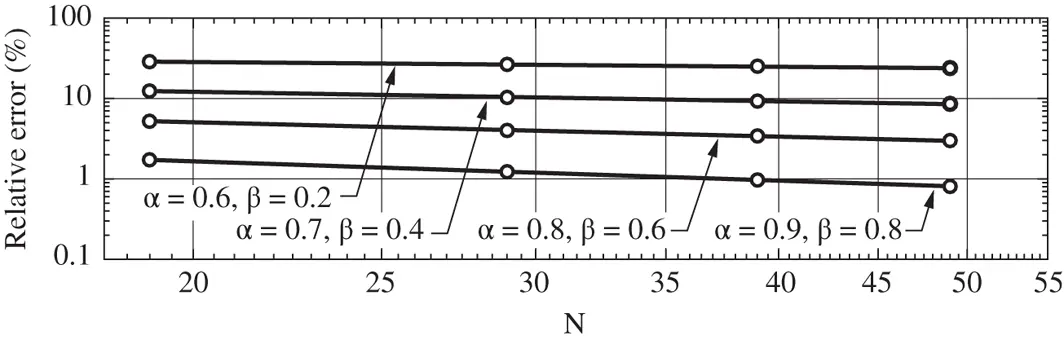
Figure 1.10 Relative error in energy norm. 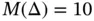 ,
, 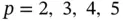 .
.
Читать дальше

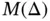
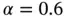
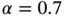
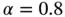
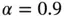
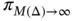
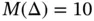 ,
, 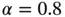 is:
is: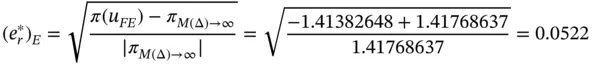
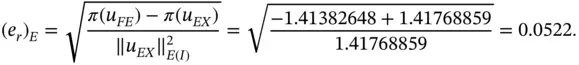
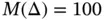 ,
, 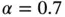 .
.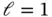 ,
, 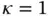 ,
, 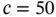 and exact solutions corresponding to
and exact solutions corresponding to 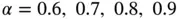 , see eq. (1.104). Using a sequence of uniform finite element meshes with
, see eq. (1.104). Using a sequence of uniform finite element meshes with 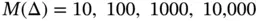 and
and 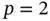 assigned to each element, the results shown in Fig. 1.9are obtained. The values of β were computed by linear regression using eq. (1.101). We observe that
assigned to each element, the results shown in Fig. 1.9are obtained. The values of β were computed by linear regression using eq. (1.101). We observe that 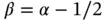 . This is consistent with the asymptotic estimate given by eq. (1.91).
. This is consistent with the asymptotic estimate given by eq. (1.91).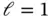 ,
, 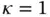 ,
, 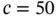 and exact solutions corresponding to
and exact solutions corresponding to 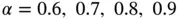 , see eq. (1.104). Using a uniform finite element mesh with
, see eq. (1.104). Using a uniform finite element mesh with 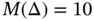 and
and 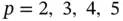 assigned to each element, the results shown in Fig. 1.10are obtained. The values of β were computed by linear regression using eq. (1.101). We observe that
assigned to each element, the results shown in Fig. 1.10are obtained. The values of β were computed by linear regression using eq. (1.101). We observe that 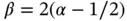 , that is, the rate of convergence is twice that in Example 1.11. This is consistent with the theoretical results in [22, 84]: The rate of p ‐convergence is at least twice the rate of h ‐convergence when the singular point is a nodal point.
, that is, the rate of convergence is twice that in Example 1.11. This is consistent with the theoretical results in [22, 84]: The rate of p ‐convergence is at least twice the rate of h ‐convergence when the singular point is a nodal point.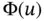 and the corresponding extraction function
and the corresponding extraction function 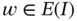 . The extracted value of the QoI is
. The extracted value of the QoI is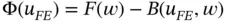

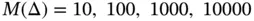 ,
, 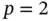 .
.
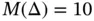 ,
, 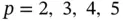 .
.










