Barna Szabó - Finite Element Analysis
Здесь есть возможность читать онлайн «Barna Szabó - Finite Element Analysis» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Finite Element Analysis
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Finite Element Analysis: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Finite Element Analysis»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.

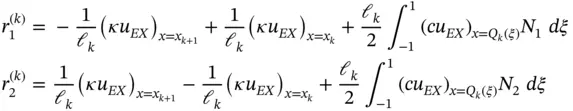
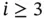 we have:
we have: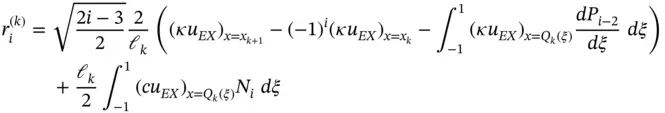
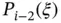 is the Legendre polynomial of degree
is the Legendre polynomial of degree 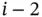 and eq. (D.10) was used.
and eq. (D.10) was used.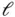 . When κ and c are both constants then
. When κ and c are both constants then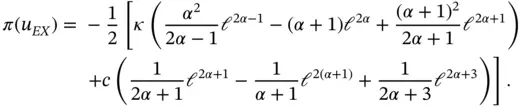
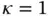 ,
, 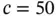 and
and 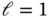 and various values of α are shown in Table 1.2.
and various values of α are shown in Table 1.2.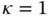 ,
, 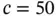 and
and 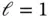 .
.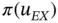
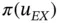
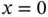 . In the range
. In the range 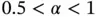 the first derivative in the point
the first derivative in the point  is infinity. This range of α has considerable practical importance because the exact solutions of two‐ and three‐dimensional problems often have analogous terms.
is infinity. This range of α has considerable practical importance because the exact solutions of two‐ and three‐dimensional problems often have analogous terms.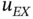 are finite. Therefore
are finite. Therefore 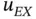 can be approximated by Taylor series about any point of the domain
can be approximated by Taylor series about any point of the domain 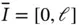 . It is known that the error term of a Taylor series truncated at polynomial degree p is bounded by the
. It is known that the error term of a Taylor series truncated at polynomial degree p is bounded by the 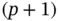 th derivative of
th derivative of 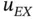 :
: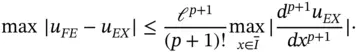
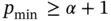 then
then 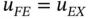 .
.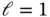 ,
, 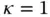 ,
,  and exact solutions in the form of eq. (1.104)corresponding to
and exact solutions in the form of eq. (1.104)corresponding to 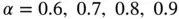 . We will use a sequence of uniform finite element meshes with
. We will use a sequence of uniform finite element meshes with 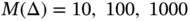 and
and 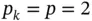 assigned to all elements. We are interested in the relationship between the estimated and true relative errors. The computed values of the potential energy and their estimated limit values computed by means of eq. (1.99)are listed in Table 1.3. These are comparable to the exact values of the potential energy listed in Table 1.2. The estimated limit values of the potential energy are denoted by
assigned to all elements. We are interested in the relationship between the estimated and true relative errors. The computed values of the potential energy and their estimated limit values computed by means of eq. (1.99)are listed in Table 1.3. These are comparable to the exact values of the potential energy listed in Table 1.2. The estimated limit values of the potential energy are denoted by 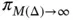 .
.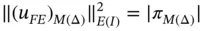
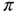 . Uniform mesh refinement,
. Uniform mesh refinement, 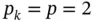 for all elements.
for all elements.










