and the exact value of the QoI is
(1.110) 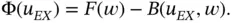
Subtracting eq. (1.109)from eq. (1.110)we get
(1.111) 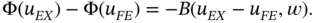
We define a function 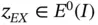 such that
such that
(1.112) 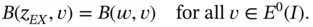
This operation projects 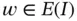 onto the space
onto the space 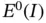 . Letting
. Letting 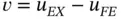 we get:
we get:
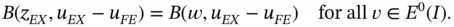
We will write this as
(1.113) 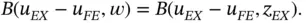
Next we define  such that
such that
(1.114) 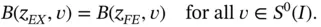
This operation projects 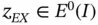 onto the space
onto the space 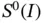 . By Galerkin's orthogonality condition (see Theorem 1.3) we have
. By Galerkin's orthogonality condition (see Theorem 1.3) we have
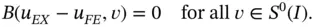
Therefore, letting 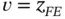 , we write eq. (1.113)as
, we write eq. (1.113)as
(1.115) 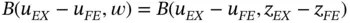
and we can write eq. (1.111)as
(1.116) 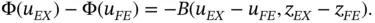
Therefore the error in the extracted data is
(1.117) 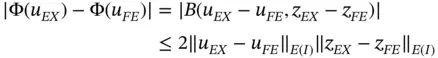
where we used the Schwarz inequality, see Section A.3in the appendix.
The function 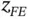 made it possible to write the error in the QoI in this form. It does not have to be computed.
made it possible to write the error in the QoI in this form. It does not have to be computed.
Inequality (1.117)serves to explain why the error in the extracted data can converge to zero faster than the error in energy norm: If 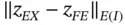 is of comparable magnitude to
is of comparable magnitude to 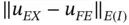 then the error in the extracted data is of comparable magnitude to the error in the strain energy, that is, the error in energy norm squared. But, as seen in Example 1.9, where w was much smoother than
then the error in the extracted data is of comparable magnitude to the error in the strain energy, that is, the error in energy norm squared. But, as seen in Example 1.9, where w was much smoother than 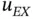 , it can be much smaller. In the exceptional case when the extraction function is Green's function, the error is zero.
, it can be much smaller. In the exceptional case when the extraction function is Green's function, the error is zero.
1.6 The choice of discretization in 1D
In an ideal discretization the error (in energy norm) associated with each element would be the same. This ideal discretization can be approximated by automated adaptive methods in which the discretization is modified based on feedback information from previously obtained finite element solutions. Alternatively, based on a general understanding of the relationship between regularity and discretization, and understanding the strengths and limitations of the software tools available to them, analysts can formulate very efficient discretization schemes.
1.6.1 The exact solution lies in 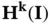 ,
, 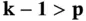
When the solution is smooth then the most efficient finite element discretization scheme is uniform mesh and high polynomial degree. However, all implementations of finite element analysis software have limitations on how high the polynomial degree is allowed to be and therefore it may not be possible to increase the polynomial degree sufficiently to achieve the desired accuracy. In such cases the mesh has to be refined. Uniform refinement may not be optimal in all cases, however. Consider, for example, the following problem:
(1.118) 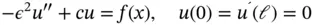
where 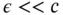 , and f is a smooth function. Intuitively, when
, and f is a smooth function. Intuitively, when 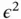 is small then the solution will be close to
is small then the solution will be close to 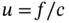 however, because of the boundary condition
however, because of the boundary condition 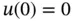 , has to be satisfied, the function
, has to be satisfied, the function 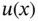 will change sharply over some interval
will change sharply over some interval 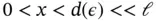 .
.
Letting 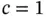 and
and 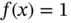 the exact solution of this problem is
the exact solution of this problem is
Читать дальше

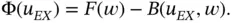
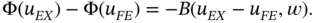
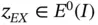 such that
such that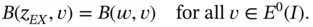
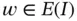 onto the space
onto the space 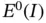 . Letting
. Letting 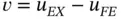 we get:
we get: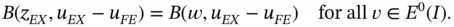
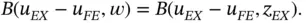
 such that
such that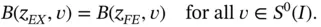
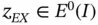 onto the space
onto the space 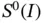 . By Galerkin's orthogonality condition (see Theorem 1.3) we have
. By Galerkin's orthogonality condition (see Theorem 1.3) we have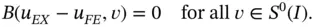
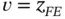 , we write eq. (1.113)as
, we write eq. (1.113)as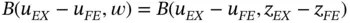
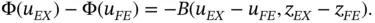
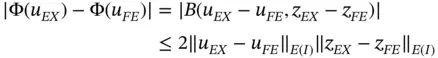
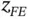 made it possible to write the error in the QoI in this form. It does not have to be computed.
made it possible to write the error in the QoI in this form. It does not have to be computed.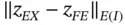 is of comparable magnitude to
is of comparable magnitude to 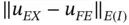 then the error in the extracted data is of comparable magnitude to the error in the strain energy, that is, the error in energy norm squared. But, as seen in Example 1.9, where w was much smoother than
then the error in the extracted data is of comparable magnitude to the error in the strain energy, that is, the error in energy norm squared. But, as seen in Example 1.9, where w was much smoother than 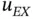 , it can be much smaller. In the exceptional case when the extraction function is Green's function, the error is zero.
, it can be much smaller. In the exceptional case when the extraction function is Green's function, the error is zero.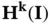 ,
, 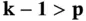
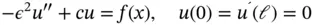
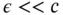 , and f is a smooth function. Intuitively, when
, and f is a smooth function. Intuitively, when 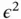 is small then the solution will be close to
is small then the solution will be close to 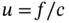 however, because of the boundary condition
however, because of the boundary condition 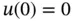 , has to be satisfied, the function
, has to be satisfied, the function 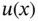 will change sharply over some interval
will change sharply over some interval 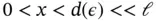 .
.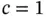 and
and 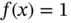 the exact solution of this problem is
the exact solution of this problem is










