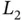1 Cover
2 Preface
3 Acknowledgments
4 1 Introduction 1.1 Preliminaries 1.2 Trinities for Second‐Order PDEs 1.3 PDEs in, Further Classifications 1.4 Differential Operators, Superposition 1.5 Some Equations of Mathematical Physics
5 2 Mathematical Tools 2.1 Vector Spaces 2.2 Function Spaces 2.3 Some Basic Inequalities 2.4 Fundamental Solution of PDEs1 2.5 The Weak/Variational Formulation 2.6 A Framework for Analytic Solution in 1d 2.7 An Abstract Framework 2.8 Exercises
6 3 Polynomial Approximation/Interpolation in 1 d 3.1 Finite Dimensional Space of Functions on an Interval 3.2 An Ordinary Differential Equation (ODE) 3.3 A Galerkin Method for (BVP) 3.4 Exercises 3.5 Polynomial Interpolation in 1d 3.6 Orthogonal‐ and L2‐Projection 3.7 Numerical Integration, Quadrature Rule 3.8 Exercises
7 4 Linear Systems of Equations 4.1 Direct Methods 4.2 Iterative Methods 4.3 Exercises
8 5 Two‐Point Boundary Value Problems 5.1 The Finite Element Method (FEM) 5.2 Error Estimates in the Energy Norm 5.3 FEM for Convection–Diffusion–Absorption BVPs 5.4 Exercises
9 6 Scalar Initial Value Problems 6.1 Solution Formula and Stability 6.2 Finite Difference Methods for IVP 6.3 Galerkin Finite Element Methods for IVP 6.4 A Posteriori Error Estimates 6.5 A Priori Error Analysis 6.6 The Parabolic Case (a(t) ≥ 0) 6.7 Exercises
10 7 Initial Boundary Value Problems in 1 d 7.1 The Heat Equation in 1d 7.2 The Wave Equation in 1d 7.3 Convection–Diffusion Problems
11 8 Approximation in Several Dimensions8.1 Introduction 8.2 Piecewise Linear Approximation in 2d 8.3 Constructing Finite Element Spaces 8.4 The Interpolant 8.5 The L2 (Revisited) and Ritz Projections 8.6 Exercises
12 9 The Boundary Value Problems in 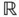 N 9.1 The Poisson Equation 9.2 Stationary Convection–Diffusion Equation 9.3 Hyperbolicity Features 9.4 Exercises
N 9.1 The Poisson Equation 9.2 Stationary Convection–Diffusion Equation 9.3 Hyperbolicity Features 9.4 Exercises
13 10 The Initial Boundary Value Problems in 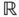 N 10.1 The Heat Equation in N 10.2 The Wave Equation in d 10.3 Exercises
N 10.1 The Heat Equation in N 10.2 The Wave Equation in d 10.3 Exercises
14 Appendix A: Appendix AAnswers to Some ExercisesAnswers to Some ExercisesChapter 1. Exercise Section 1.4.1 Chapter 1. Exercise Section 1.5.4 Chapter 2. Exercise Section 2.11 Chapter 3. Exercise Section 3.5 Chapter 3. Exercise Section 3.8 Chapter 4. Exercise Section 4.3 Chapter 5. Exercise Section 5.4 Chapter 6. Exercise Section 6.7 Chapter 7. Exercise Section 7.2.3 Chapter 7. Exercise Section 7.3.3 Chapter 9. Poisson Equation. Exercise Section 9.4 Chapter 10. IBVPs: Exercise Section 10.3
15 Appendind B: Appendind BAlgorithms and Matlab CodesAlgorithms and Matlab Codes B.1 A Matlab Code to Compute the Mass Matrix M for a Nonuniform Mesh B.2 Matlab Routine to Compute the L2‐Projection B.3 A Matlab Routine Assembling the Stiffness Matrix B.4 A Matlab Routine to Assemble the Convection Matrix B.5 Matlab Routine for Forward‐, Backward‐Euler, and Crank–Nicolson B.6 A Matlab Routine for Mass‐Matrix in 2d B.7 A Matlab Routine for a Poisson Assembler in 2d
16 Appendix C: Appendix CSample AssignmentsSample AssignmentsC.1 Assignment 1 C.2 Assignment 2
17 Appendix D: Appendix DSymbolsSymbolsD.1 Table of Symbols
18 Bibliography
19 Index
20 End User License Agreement
1 Chapter 8Table 8.1 Some one‐dimensional finite elements.Table 8.2 Some two‐dimensional finite elements with triangular elements.Table 8.3 Some two‐dimensional finite elements with quadrilateral elements.Table 8.4 Some three‐dimensional finite elements with tetrahedron elements.
1 Chapter 1 Figure 1.1 Tricomi equation: an example of a variable coefficient classifica... Figure 1.2 Outward unit normal 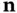 at a point
at a point 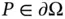 . Figure 1.3 A heat‐conducting one‐dimensional wire. Figure 1.4 A vibrating string.
. Figure 1.3 A heat‐conducting one‐dimensional wire. Figure 1.4 A vibrating string.
2 Chapter 2Figure 2.1 The hat function 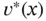 over the interval
over the interval 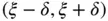 .Figure 2.2 Illustrating the existence of a unique solution for (V) and (M)....
.Figure 2.2 Illustrating the existence of a unique solution for (V) and (M)....
3 Chapter 3Figure 3.1 Linear Lagrange basis functions for 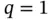 .Figure 3.2 The linear interpolant
.Figure 3.2 The linear interpolant 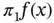 on a single interval.Figure 3.3 An example of a function in
on a single interval.Figure 3.3 An example of a function in 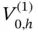 .Figure 3.4 A general piecewise linear basis function
.Figure 3.4 A general piecewise linear basis function 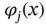 .Figure 3.5 A partition of
.Figure 3.5 A partition of 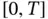 .Figure 3.6 Piecewise linear basis functions.Figure 3.7
.Figure 3.6 Piecewise linear basis functions.Figure 3.7 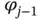 and
and 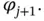 Figure 3.8
Figure 3.8 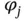 and
and 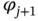 .Figure 3.9 (a) Linear interpolation and (b) basis functions for
.Figure 3.9 (a) Linear interpolation and (b) basis functions for 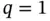 .Figure 3.10 Linear Lagrange basis functions for
.Figure 3.10 Linear Lagrange basis functions for 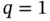 .Figure 3.11 Piecewise linear interpolant
.Figure 3.11 Piecewise linear interpolant 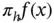 of
of 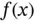 .Figure 3.12 Linear Lagrange basis functions for
.Figure 3.12 Linear Lagrange basis functions for 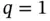 on subinterval
on subinterval 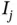 .Figure 3.13 Example of a projection onto
.Figure 3.13 Example of a projection onto  .Figure 3.14 An example of a function
.Figure 3.14 An example of a function  and its
and its 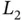
Читать дальше

 N 9.1 The Poisson Equation 9.2 Stationary Convection–Diffusion Equation 9.3 Hyperbolicity Features 9.4 Exercises
N 9.1 The Poisson Equation 9.2 Stationary Convection–Diffusion Equation 9.3 Hyperbolicity Features 9.4 Exercises N 10.1 The Heat Equation in N 10.2 The Wave Equation in d 10.3 Exercises
N 10.1 The Heat Equation in N 10.2 The Wave Equation in d 10.3 Exercises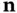 at a point
at a point 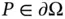 . Figure 1.3 A heat‐conducting one‐dimensional wire. Figure 1.4 A vibrating string.
. Figure 1.3 A heat‐conducting one‐dimensional wire. Figure 1.4 A vibrating string.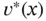 over the interval
over the interval 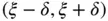 .Figure 2.2 Illustrating the existence of a unique solution for (V) and (M)....
.Figure 2.2 Illustrating the existence of a unique solution for (V) and (M)....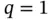 .Figure 3.2 The linear interpolant
.Figure 3.2 The linear interpolant 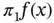 on a single interval.Figure 3.3 An example of a function in
on a single interval.Figure 3.3 An example of a function in 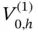 .Figure 3.4 A general piecewise linear basis function
.Figure 3.4 A general piecewise linear basis function 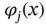 .Figure 3.5 A partition of
.Figure 3.5 A partition of 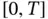 .Figure 3.6 Piecewise linear basis functions.Figure 3.7
.Figure 3.6 Piecewise linear basis functions.Figure 3.7 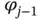 and
and 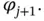 Figure 3.8
Figure 3.8 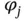 and
and 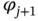 .Figure 3.9 (a) Linear interpolation and (b) basis functions for
.Figure 3.9 (a) Linear interpolation and (b) basis functions for 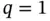 .Figure 3.10 Linear Lagrange basis functions for
.Figure 3.10 Linear Lagrange basis functions for 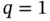 .Figure 3.11 Piecewise linear interpolant
.Figure 3.11 Piecewise linear interpolant 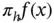 of
of 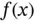 .Figure 3.12 Linear Lagrange basis functions for
.Figure 3.12 Linear Lagrange basis functions for 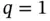 on subinterval
on subinterval 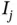 .Figure 3.13 Example of a projection onto
.Figure 3.13 Example of a projection onto 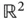 .Figure 3.14 An example of a function
.Figure 3.14 An example of a function 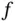 and its
and its