1 Cover
2 Title Page Generalized Ordinary Differential Equations in Abstract Spaces and Applications Edited by Everaldo M. Bonotto Universidade de São Paulo São Carlos, SP, Brazil Márcia Federson Universidade de São Paulo São Carlos, SP, Brazil Jaqueline G. Mesquita Universidade de Brasília Brasília, DF, Brazil
3 Copyright
4 Dedication
5 List of Contributors
6 Foreword
7 Preface
8 1 Preliminaries 1.1 Regulated Functions 1.2 Functions of Bounded ‐Variation 1.3 Kurzweil and Henstock Vector Integrals Appendix 1.A: The McShane Integral
9 2 The Kurzweil Integral 2.1 The Main Background 2.2 Basic Properties 2.3 Notes on Kapitza Pendulum
10 3 Measure Functional Differential Equations 3.1 Measure FDEs 3.2 Impulsive Measure FDEs 3.3 Functional Dynamic Equations on Time Scales 3.4 Averaging Methods 3.5 Continuous Dependence on Time Scales
11 4 Generalized Ordinary Differential Equations 4.1 Fundamental Properties 4.2 Relations with Measure Differential Equations 4.3 Relations with Measure FDEs
12 5 Basic Properties of Solutions 5.1 Local Existence and Uniqueness of Solutions 5.2 Prolongation and Maximal Solutions
13 6 Linear Generalized Ordinary Differential Equations 6.1 The Fundamental Operator 6.2 A Variation-of-Constants Formula 6.3 Linear Measure FDEs 6.4 A Nonlinear Variation-of-Constants Formula for Measure FDEs
14 7 Continuous Dependence on Parameters 7.1 Basic Theory for Generalized ODEs 7.2 Applications to Measure FDEs
15 8 Stability Theory 8.1 Variational Stability for Generalized ODEs 8.2 Lyapunov Stability for Generalized ODEs 8.3 Lyapunov Stability for MDEs 8.4 Lyapunov Stability for Dynamic Equations on Time Scales 8.5 Regular Stability for Generalized ODEs
16 9 Periodicity 9.1 Periodic Solutions and Floquet's Theorem 9.2 ( θ, T )-Periodic Solutions
17 10 Averaging Principles 10.1 Periodic Averaging Principles 10.2 Nonperiodic Averaging Principles
18 11 Boundedness of Solutions 11.1 Bounded Solutions and Lyapunov Functionals 11.2 An Application to MDEs
19 12 Control Theory 12.1 Controllability and Observability 12.2 Applications to ODEs
20 13 Dichotomies 13.1 Basic Theory for Generalized ODEs 13.2 Boundedness and Dichotomies 13.3 Applications to MDEs 13.4 Applications to IDEs
21 14 Topological Dynamics 14.1 The Compactness of the Class 14.2 Existence of a Local Semidynamical System 14.3 Existence of an Impulsive Semidynamical System 14.4 LaSalle's Invariance Principle 14.5 Recursive Properties
22 15 Applications to Functional Differential Equations of Neutral Type 15.1 Drops of History 15.2 FDEs of Neutral Type with Finite Delay
23 References
24 List of Symbols
25 Index
26 End User License Agreement
1 Chapter 9Figure 9.1 Trajectory of 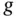 .Figure 9.2 Trajectory of
.Figure 9.2 Trajectory of 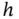 .
.
1 Cover
2 Table of Contents
3 Title Page Generalized Ordinary Differential Equations in Abstract Spaces and Applications Edited by Everaldo M. Bonotto Universidade de São Paulo São Carlos, SP, Brazil Márcia Federson Universidade de São Paulo São Carlos, SP, Brazil Jaqueline G. Mesquita Universidade de Brasília Brasília, DF, Brazil
4 Copyrigt
5 Dedication
6 List of Contributors
7 Foreword
8 Preface
9 Begin Reading
10 References
11 List of Symbols
12 Index
13 End User License Agreement
1 iii
2 iv
3 v
4 xi
5 xii
6 xiii
7 xiv
8 xv
9 xvii
10 xviii
11 xix
12 xx
13 xxi
14 1
15 2
16 3
17 4
18 5
19 6
20 7
21 8
22 9
23 10
24 11
25 12
26 13
27 14
28 15
29 16
30 17
31 18
32 19
33 20
34 21
35 22
36 23
37 24
38 25
39 26
40 27
41 28
42 29
43 30
44 31
45 32
46 33
47 34
48 35
49 36
50 37
51 38
52 39
53 40
54 41
55 42
56 43
57 44
58 45
59 46
60 47
61 48
62 49
63 50
64 51
65 52
66 53
67 54
68 55
69 56
70 57
71 58
72 59
73 60
74 61
75 62
76 63
77 64
78 65
79 66
80 67
81 68
82 69
83 70
84 71
85 72
86 73
87 74
88 75
89 76
90 77
91 78
92 79
93 80
94 81
95 82
96 83
97 84
98 85
99 86
100 87
101 88
102 89
103 90
104 91
105 92
106 93
107 94
108 95
109 96
110 97
111 98
112 99
113 100
114 101
115 102
116 103
117 104
118 105
119 106
120 107
121 108
122 109
123 110
124 111
125 112
126 113
127 114
128 115
129 116
130 117
131 118
132 119
133 120
134 121
135 122
136 123
137 124
138 125
139 126
140 127
141 128
142 129
143 130
144 131
145 132
146 133
147 134
148 135
149 136
150 137
151 138
152 139
153 140
154 141
155 142
156 143
157 145
158 146
159 147
160 148
161 149
162 150
163 151
164 152
165 153
166 154
167 155
168 156
169 157
170 158
171 159
172 160
173 161
174 162
175 163
176 164
177 165
178 166
179 167
180 168
181 169
182 170
183 171
184 173
185 174
186 175
187 176
188 177
189 178
190 179
191 180
192 181
193 182
194 183
195 184
196 185
197 186
198 187
199 188
200 189
201 190
202 191
203 192
204 193
205 194
206 195
207 196
208 197
209 198
210 199
211 200
212 201
213 202
214 203
215 204
216 205
217 206
218 207
219 208
220 209
221 210
222 211
223 212
224 213
225 214
226 215
227 216
228 217
229 218
230 219
231 220
232 221
233 222
234 223
235 224
236 225
237 226
238 227
239 228
240 229
241 230
242 231
243 232
244 233
245 234
246 235
247 236
248 237
249 238
250 239
251 240
252 241
253 242
254 243
255 244
256 245
257 246
258 247
259 248
260 249
261 250
262 251
263 252
264 253
265 254
266 255
267 256
268 257
269 258
270 259
271 260
272 261
273 262
274 263
275 264
276 265
277 266
278 267
279 268
280 269
281 270
282 271
283 272
284 273
285 274
286 275
287 276
288 277
289 278
290 279
291 280
292 281
293 282
294 283
295 284
296 285
297 286
298 287
299 288
300 289
301 290
302 291
303 292
304 293
305 294
Читать дальше

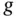 .Figure 9.2 Trajectory of
.Figure 9.2 Trajectory of 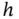 .
.










