1 Cover
2 Title Page SCIENCES Mathematics , Field Director – Nikolaos Limnios Algebra and Geometry, Subject Head – Abdenacer Makhlouf
3 Copyright First published 2021 in Great Britain and the United States by ISTE Ltd and John Wiley & Sons, Inc. Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address: ISTE Ltd 27-37 St George’s Road London SW19 4EU UK www.iste.co.uk John Wiley & Sons, Inc. 111 River Street Hoboken, NJ 07030 USA www.wiley.com © ISTE Ltd 2021 The rights of Abdenacer Makhlouf to be identified as the author of this work have been asserted by him in accordance with the Copyright, Designs and Patents Act 1988. Library of Congress Control Number: 2021942616 British Library Cataloguing-in-Publication Data A CIP record for this book is available from the British Library ISBN 978-1-78945–018-7 ERC code: PE1 Mathematics PE1_2 Algebra PE1_5 Lie groups, Lie algebras PE1_12 Mathematical physics
4 Preface
5 1 Algebraic Background for Numerical Methods, Control Theory and Renormalization 1.1. Introduction 1.2. Hopf algebras: general properties 1.3. Connected Hopf algebras 1.4. Pre-Lie algebras 1.5. Algebraic operads 1.6. Pre-Lie algebras (continued) 1.7. Other related algebraic structures 1.8. References
6 2 From Iterated Integrals and Chronological Calculus to Hopf and Rota–Baxter Algebras 2.1. Introduction 2.2. Generalized iterated integrals 2.3. Advances in chronological calculus 2.4. Rota–Baxter algebras 2.5. References
7 3 Noncommutative Symmetric Functions, Lie Series and Descent Algebras 3.1. Introduction 3.2. Classical symmetric functions 3.3. Noncommutative symmetric functions 3.4. Lie series and Lie idempotents 3.5. Lie idempotents as noncommutative symmetric functions 3.6. Decompositions of the descent algebras 3.7. Decompositions of the tensor algebra 3.8. General deformations 3.9. Lie quasi-idempotents as Lie polynomials 3.10. Permutations and free quasi-symmetric functions 3.11. Packed words and word quasi-symmetric functions 3.12. References
8 4 From Runge–Kutta Methods to Hopf Algebras of Rooted Trees 4.1. Numerical integration methods for ordinary differential equations 4.2. Algebraic theory of Runge–Kutta methods 4.3. B-series and related formal expansions 4.4. Hopf algebras of rooted trees 4.5. References
9 5 Combinatorial Algebra in Controllability and Optimal Control 5.1. Introduction 5.2. Analytic foundations 5.3. Controllability and optimality 5.4. Product expansions and realizations 5.5. References
10 6 Algebra is Geometry is Algebra – Interactions Between Hopf Algebras, Infinite Dimensional Geometry and Application 6.1. The Butcher group and the Connes–Kreimer algebra 6.2. Character groups of graded and connected Hopf algebras 6.3. Controlled groups of characters 6.4. Appendix: Calculus in locally convex spaces 6.5. References
11 List of Authors
12 Index
1 Chapter 5 Figure 5.1.Parallel parking a car (bicycle). For a color version of this figure... Figure 5.2. The states of the bicycle Figure 5.3. An inverted pendulum Figure 5.4. Open-loop and closed-loop controls with a feedback controller K Figure 5.5.Parallel parking a car (bicycle). For a color version of this figure... Figure 5.6.Pontryagin maximum principle. For a color version of this figure, se... Figure 5.7. Needle variations also scaled by amplitude Figure 5.8. More complex family of control variations
1 Chapter 4 Table 4.1. Functions 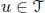 associated with rooted trees with up to four vertices Table 4.2. Elementary differentials Fu and the values of u ! and σ(u) for rooted ...
associated with rooted trees with up to four vertices Table 4.2. Elementary differentials Fu and the values of u ! and σ(u) for rooted ...
2 Chapter 6 Table 6.1.Standard examples for growth families (Dahmen and Schmeding 2018, Pro...
1 Cover
2 Table of Contents
3 Title page
4 Copyright First published 2021 in Great Britain and the United States by ISTE Ltd and John Wiley & Sons, Inc. Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address: ISTE Ltd 27-37 St George’s Road London SW19 4EU UK www.iste.co.uk John Wiley & Sons, Inc. 111 River Street Hoboken, NJ 07030 USA www.wiley.com © ISTE Ltd 2021 The rights of Abdenacer Makhlouf to be identified as the author of this work have been asserted by him in accordance with the Copyright, Designs and Patents Act 1988. Library of Congress Control Number: 2021942616 British Library Cataloguing-in-Publication Data A CIP record for this book is available from the British Library ISBN 978-1-78945–018-7 ERC code: PE1 Mathematics PE1_2 Algebra PE1_5 Lie groups, Lie algebras PE1_12 Mathematical physics
5 Preface
6 Begin Reading
7 List of Authors
8 Index
9 End User License Agreement
1 v
2 xi
3 xii
4 1
5 2
6 3
7 4
8 5
9 6
10 7
11 8
12 9
13 10
14 11
15 12
16 13
17 14
18 15
19 16
20 17
21 18
22 19
23 20
24 21
25 22
26 23
27 24
28 25
29 26
30 27
31 28
32 29
33 30
34 31
35 32
36 33
37 34
38 35
39 36
40 37
41 38
42 39
43 40
44 41
45 42
46 43
47 44
48 45
49 46
50 47
51 48
52 49
53 50
54 51
55 52
56 53
57 55
58 56
59 57
60 58
61 59
62 60
63 61
64 62
65 63
66 64
67 65
68 66
69 67
70 68
71 69
72 70
73 71
74 72
75 73
76 74
77 75
78 76
79 77
80 78
81 79
82 80
83 81
84 82
85 83
86 84
87 85
88 86
89 87
90 88
91 89
92 90
93 91
94 92
95 93
96 94
97 95
98 96
99 97
100 98
101 99
102 100
103 101
104 102
105 103
106 104
107 105
108 106
109 107
110 108
111 109
112 110
113 111
114 112
115 113
116 114
117 115
118 116
119 117
120 118
121 119
122 120
123 121
124 122
125 123
126 124
127 125
128 126
129 127
130 128
131 129
132 130
133 131
134 132
135 133
136 134
Читать дальше

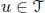 associated with rooted trees with up to four vertices Table 4.2. Elementary differentials Fu and the values of u ! and σ(u) for rooted ...
associated with rooted trees with up to four vertices Table 4.2. Elementary differentials Fu and the values of u ! and σ(u) for rooted ...










