1.2.4. Bialgebras and Hopf algebras
A (unital and counital) bialgebra is a vector space ℋ endowed with a structure of unital algebra ( m , ε ) and a structure of counital coalgebra (Δ, ε ), which are compatible. The compatibility requirement is that Δ is an algebra morphism (or equivalently that m is a coalgebra morphism), ε is an algebra morphism and u is a coalgebra morphism. It is expressed by the commutativity of the three following diagrams:
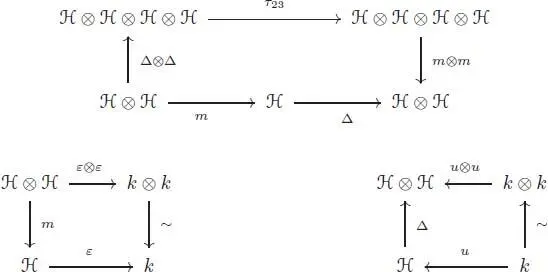
A Hopf algebra is a bialgebra ℋ together with a linear map S : ℋ → ℋ, called the antipode , such that the following diagram commutes:
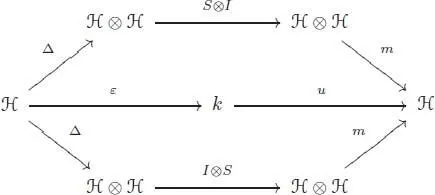
In Sweedler’s notation, it reads:
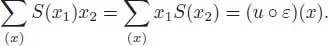
In other words, the antipode is an inverse of the identity I for the convolution product on 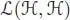 . The unit for the convolution is the map u ∘ ε .
. The unit for the convolution is the map u ∘ ε .
A primitive element in a bialgebra ℋ is an element x , such that Δ x = x ⊗1 + 1⊗ x . A grouplike element is a nonzero element x , such that Δ x = x ⊗ x . Note that grouplike elements make sense in any coalgebra.
A bi-ideal in a bialgebra ℋ is a two-sided ideal, which is also a two-sided coideal. A Hopf ideal in a Hopf algebra ℋ is a bi-ideal J , such that S ( J ) ⊂ J .
1.2.5. Some simple examples of Hopf algebras
1.2.5.1. The Hopf algebra of a group
Let G be a group, and let kG be the group algebra (over the field k ). It is by definition the vector space freely generated by the elements of G : the product of G extends uniquely to a bilinear map from kG × kG into kG , hence, a multiplication m : kG ⊗ kG → kG , which is associative. The neutral element of G gives the unit for m . The space kG is also endowed with a counital coalgebra structure, given by:
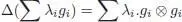
and:
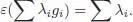
This defines the coalgebra of the set G : it does not take into account the extra group structure on G , as the algebra structure does.
PROPOSITION 1.3.– The vector space kG endowed with the algebra and coalgebra structures defined above is a Hopf algebra. The antipode is given by :
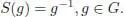
PROOF.– The compatibility of the product and the coproduct is an immediate consequence of the following computation: for any g , h ∈ G , we have:
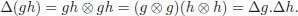
Now, m ( S ⊗ I )Δ( g ) = g -1 g = e and similarly for m ( I ⊗ S )Δ( g ). But, e = u ∘ ε ( g ) for any g ∈ G , so the map S is indeed the antipode. □
REMARK 1.1.– If G were only a semigroup, the same construction would lead to a bialgebra structure on kG: the Hopf algebra structure (i.e. the existence of an antipode) reflects the group structure (the existence of the inverse). We have S2 = I in this case; however, the involutivity of the antipode is not true for general Hopf algebras .
There is a natural structure of cocommutative Hopf algebra on the tensor algebra T ( V ) of any vector space V . Namely, we define the coproduct Δ as the unique algebra morphism from T ( V ) into T ( V ) ⊗ T ( V ), such that:
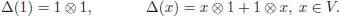
We define the counit as the algebra morphism, such that ε (1) = 1 and 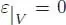 . This endows T ( V ) with a cocommutative bialgebra structure. We claim that the principal anti-automorphism:
. This endows T ( V ) with a cocommutative bialgebra structure. We claim that the principal anti-automorphism:
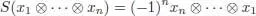
verifies the axioms of an antipode, so that T ( V ) is indeed a Hopf algebra. For x ∈ V , we have S ( x ) = – x ; hence, S * I ( x ) = I * S ( x ) = 0. As V generates T ( V ) as an algebra, it is easy to conclude.
1.2.5.3. Enveloping algebras
Let 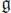 be a Lie algebra. The universal enveloping algebra is the quotient of the tensor algebra
be a Lie algebra. The universal enveloping algebra is the quotient of the tensor algebra 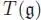 by the ideal J generated by x ⊗ y — y ⊗ x — [ x , y ],
by the ideal J generated by x ⊗ y — y ⊗ x — [ x , y ], 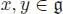 .
.
LEMMA 1.1.– J is a Hopf ideal, that is , Δ( J ) ⊂ ℋ ⊗ J + J ⊗ ℋ and S ( J ) ⊂ J .
PROOF.– The ideal J is generated by primitive elements (according to Proposition 1.5 below), and any ideal generated by primitive elements is a Hopf ideal (very easy and left to the reader). □
The quotient of a Hopf algebra by a Hopf ideal is a Hopf algebra. Hence, the universal enveloping algebra 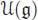 is a cocommutative Hopf algebra.
is a cocommutative Hopf algebra.
1.2.6. Some basic properties of Hopf algebras
In the proposition below we summarize the main properties of the antipode in a Hopf algebra:
PROPOSITION 1.4.– (see Sweedler (1969, Proposition 4.0.1)). Let ℋ be a Hopf algebra with multiplication m, comultiplication Δ, unit u : 1 ↦ 1, counit ε and antipode S. Then :
Читать дальше



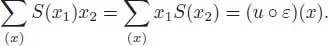
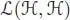 . The unit for the convolution is the map u ∘ ε .
. The unit for the convolution is the map u ∘ ε .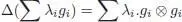
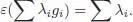
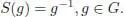
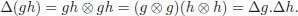
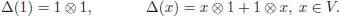
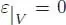 . This endows T ( V ) with a cocommutative bialgebra structure. We claim that the principal anti-automorphism:
. This endows T ( V ) with a cocommutative bialgebra structure. We claim that the principal anti-automorphism: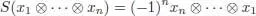
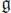 be a Lie algebra. The universal enveloping algebra is the quotient of the tensor algebra
be a Lie algebra. The universal enveloping algebra is the quotient of the tensor algebra 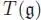 by the ideal J generated by x ⊗ y — y ⊗ x — [ x , y ],
by the ideal J generated by x ⊗ y — y ⊗ x — [ x , y ], 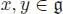 .
.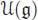 is a cocommutative Hopf algebra.
is a cocommutative Hopf algebra.










