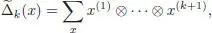1 1) S ∘ u = u and ε o S = ε.
2 2) S is an algebra antimorphism and a coalgebra antimorphism, that is, if denotes the flip, we have:
3 3) If ℋ is commutative or cocommutative, then S2 = I.
For a detailed proof, see Kassel (1995).
PROPOSITION 1.5.–
1 1) If x is a primitive element, then S(x) = –x.
2 2) The linear subspace Prim ℋ of primitive elements in ℋ is a Lie algebra.
PROOF.– If x is primitive, then ( ε ⊗ ε ) ∘ Δ( x ) = 2 ε ( x ). On the contrary, ( ε ⊗ ε ) ∘ Δ( x ) = ε ( x ), so ε ( x ) = 0. Then:
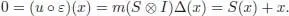
Now let x and y be the primitive elements of ℋ. Then, we can easily compute:
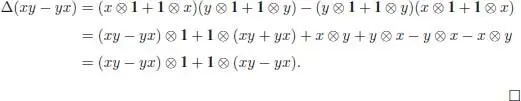
1.3. Connected Hopf algebras
We introduce the crucial property of connectedness for bialgebras. The main interest resides in the possibility of implementing recursive procedures in connected bialgebras, the induction taking place with respect to a filtration or a grading. An important example of these techniques is the recursive construction of the antipode, which then “comes for free”, showing that any connected bialgebra is in fact a connected Hopf algebra.
1.3.1. Connected graded bialgebras
A graded Hopf algebra on k is a graded k -vector space:
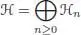
endowed with a product m : ℋ ⊗ ℋ → ℋ, a coproduct Δ : ℋ ↑ ℋ ⊗ ℋ, a unit u : k → ℋ , a counit ε : ℋ → k and an antipode S : ℋ → ℋ, fulfilling the usual axioms of a Hopf algebra, and such that:
[1.1] 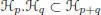
[1.2] 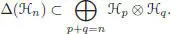
If we do not ask for the existence of an antipode ℋ, we get the definition of a graded bialgebra . In a graded bialgebra ℋ, we will consider the increasing filtration:
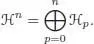
It is an easy exercise (left to the reader) to prove that the unit u and the counit ε are degree zero maps, that is, 1∈ ℋ 0and ε (ℋ n) = {0} for n ≥ 1. We can also show that the antipode S , when it exists, is also of degree zero, that is, S (ℋ n ) ⊂ ℋ n. It can be proven as follows: let S ′ : ℋ → ℋ be defined, so that S ’( x ) is the n thhomogeneous component of S ( x ) when x is homogeneous of degree n . We can write down the coproduct Δ( x ) with Sweedler’s notation:
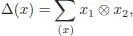
where x 1and x 2are the homogeneous of degree, say, k and n — k . We then have:
[1.3] 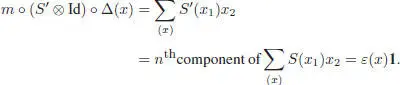
Similarly, m ∘ (Id ⊗ S ′) ∘ Δ( x ) = ε ( x ) 1. By uniqueness of the antipode, we then get S ’ = S .
Suppose that ℋ is connected , that is, ℋ 0is one-dimensional. Then, we have:
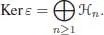
PROPOSITION 1.6.– For any x ∈ ℋ n, n ≥ 1, we can write:
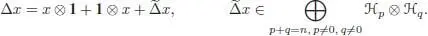
The map 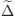 is coassociative on Ker ε and
is coassociative on Ker ε and 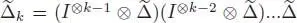 sends ℋ n into (ℋ n-k) ⊗k + 1.
sends ℋ n into (ℋ n-k) ⊗k + 1.
PROOF .– Thanks to connectedness we can clearly write:
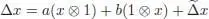
with a,b ∈ k and 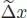 ∈ Ker ε ⊗ Ker ε . The counit property then tells us that, with k ⊗ ℋ and ℋ ⊗ k canonically identified with ℋ:
∈ Ker ε ⊗ Ker ε . The counit property then tells us that, with k ⊗ ℋ and ℋ ⊗ k canonically identified with ℋ:
[1.4] 
hence, a = b = 1. We will use the following two variants of Sweedler’s notation:
[1.5] 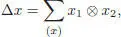
[1.6] 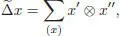
the second being relevant only for x ⊗ Ker ε . If x is homogeneous of degree n , we can suppose that the components x 1, x 2, x ′, x ″ in the expressions above are homogeneous as well, and we then have | x 1| + | x 2| = n and | x ′| + | x ″| = n . We easily compute:
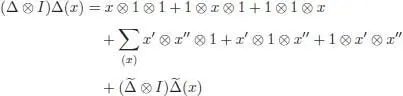
and
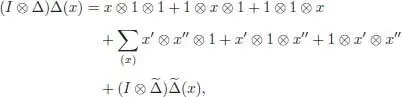
hence, the coassociativity of 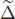 comes from the one of Δ. Finally, it is easily seen by induction on k that for any x ∈ ℋ n, we can write:
comes from the one of Δ. Finally, it is easily seen by induction on k that for any x ∈ ℋ n, we can write:
[1.7] 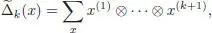
Читать дальше

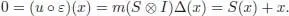
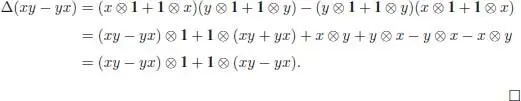
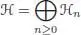
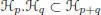
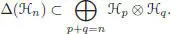
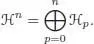
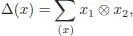
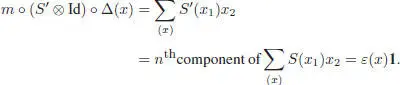
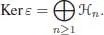
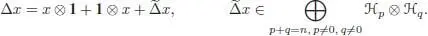
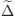 is coassociative on Ker ε and
is coassociative on Ker ε and 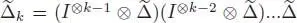 sends ℋ n into (ℋ n-k) ⊗k + 1.
sends ℋ n into (ℋ n-k) ⊗k + 1.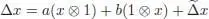
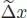 ∈ Ker ε ⊗ Ker ε . The counit property then tells us that, with k ⊗ ℋ and ℋ ⊗ k canonically identified with ℋ:
∈ Ker ε ⊗ Ker ε . The counit property then tells us that, with k ⊗ ℋ and ℋ ⊗ k canonically identified with ℋ:
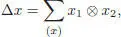
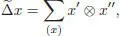
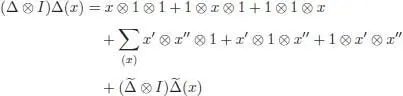
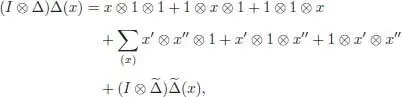
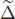 comes from the one of Δ. Finally, it is easily seen by induction on k that for any x ∈ ℋ n, we can write:
comes from the one of Δ. Finally, it is easily seen by induction on k that for any x ∈ ℋ n, we can write: