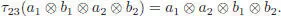Since the pioneering work of Cayley in the 19th century (Cayley 1857), we have known that rooted trees and vector fields on the affine space are closely related. Surprisingly enough, rooted trees were also revealed to be a fundamental tool for studying not only the integral curves of vector fields, but also their Runge–Kutta numerical approximations (Butcher 1963).
The rich algebraic structure of the k -vector space 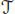 spanned by rooted trees (where k is some field of characteristic zero) can be, in a nutshell, described as follows:
spanned by rooted trees (where k is some field of characteristic zero) can be, in a nutshell, described as follows: 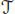 is both the free pre-Lie algebra with one generator and the free non-associative permutative algebra with one generator (Chapoton and Livernet 2001; Dzhumadil’daev and Löfwall 2002), and moreover, there are two other pre-Lie structures on
is both the free pre-Lie algebra with one generator and the free non-associative permutative algebra with one generator (Chapoton and Livernet 2001; Dzhumadil’daev and Löfwall 2002), and moreover, there are two other pre-Lie structures on 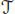 , of operadic nature, which show strong compatibility with the first pre-Lie (respectively the NAP) structure (Chapoton and Livernet 2001; Calaque et al . 2011; Manchon and Saidi 2011). The Hopf algebra of coordinates on the Butcher group (Butcher 1963), that is, the graded dual of the enveloping algebra
, of operadic nature, which show strong compatibility with the first pre-Lie (respectively the NAP) structure (Chapoton and Livernet 2001; Calaque et al . 2011; Manchon and Saidi 2011). The Hopf algebra of coordinates on the Butcher group (Butcher 1963), that is, the graded dual of the enveloping algebra 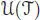 (with respect to the Lie bracket given by the first pre-Lie structure), was first investigated in Dür (1986), and intensively studied by Kreimer for renormalization purposes in Quantum Field Theory (Connes and Kreimer 1998; Kreimer 2002), see also Brouder (2000).
(with respect to the Lie bracket given by the first pre-Lie structure), was first investigated in Dür (1986), and intensively studied by Kreimer for renormalization purposes in Quantum Field Theory (Connes and Kreimer 1998; Kreimer 2002), see also Brouder (2000).
This chapter is organized as follows: the first section is devoted to general connected graded or filtered Hopf algebras, including the renormalization of their characters. The second section gives a short presentation of operads in the symmetric monoidal category of vector spaces, and the third section will treat pre-Lie algebras in some detail: in particular, we will give a “pedestrian” proof of the Chapoton-Livernet theorem on free pre-Lie algebras. In the last section, Rota-Baxter, dendriform and NAP algebras will be introduced.
1.2. Hopf algebras: general properties
We choose a base field k of characteristic zero. Most of the material here is borrowed from Manchon (2008), to which we can refer for more details.
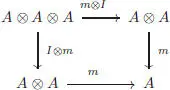
A k -algebra is by definition a k -vector space A together with a bilinear map m : A ⊗ A → A which is associative . The associativity is expressed by the commutativity of the following diagram:
The algebra A is unital if there is a unit 1in it. This is expressed by the commutativity of the following diagram:
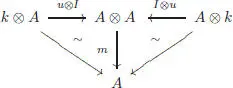
where u is the map from k to A defined by u (λ) = λ 1. The algebra A is commutative if  , where
, where  : A ⊗ A → A ⊗ A is the flip , defined by
: A ⊗ A → A ⊗ A is the flip , defined by 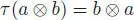 .
.
A subspace J ⊂ A is called a subalgebra (respectively a left ideal, right ideal and two-sided ideal ) of A if m ( J ⊗ J ) (respectively m ( A ⊗ J ), m ( J ⊗ A ), m ( J ⊗ A + A ⊗ J )) is included in J .
With any vector space V , we can associate its tensor algebra T ( V ). As a vector space, it is defined by:
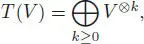
with V ⊗0= k and V ⊗ k+1:= V ⊗ V ⊗k. The product is given by the concatenation :
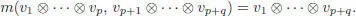
The embedding of k = V ⊗0into T ( V ) gives the unit map u . The tensor algebra T ( V ) is also called the free (unital) algebra generated by V . This algebra is characterized by the following universal property: for any linear map φ from V to a unital algebra A , there is a unique unital algebra morphism  from T ( V ) to A extending φ .
from T ( V ) to A extending φ .
Let A and B be the unital k -algebras. We put a unital algebra structure on A ⊗ B in the following way:
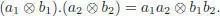
The unit element 1 A⊗Bis given by 1 A⊗ 1 B, and the associativity is clear. This multiplication is thus given by:
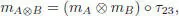
where 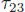 : A ⊗ B ⊗ A ⊗ B → A ⊗ A ⊗ B ⊗ B is defined by the flip of the two middle factors:
: A ⊗ B ⊗ A ⊗ B → A ⊗ A ⊗ B ⊗ B is defined by the flip of the two middle factors:
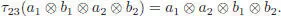
Coalgebras are the objects which are somehow dual to algebras: axioms for coalgebras are derived from axioms for algebras by reversing the arrows of the corresponding diagrams:
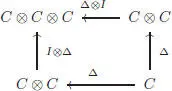
A k -coalgebra is by definition a k -vector space C together with a bilinear map Δ : C → C ⊗ C , which is coassociative . The coassociativity is expressed by the commutativity of the following diagram:
Coalgebra C is counital if there is a counit ε : C → k , such that the following diagram commutes:
Читать дальше

 spanned by rooted trees (where k is some field of characteristic zero) can be, in a nutshell, described as follows:
spanned by rooted trees (where k is some field of characteristic zero) can be, in a nutshell, described as follows: 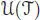 (with respect to the Lie bracket given by the first pre-Lie structure), was first investigated in Dür (1986), and intensively studied by Kreimer for renormalization purposes in Quantum Field Theory (Connes and Kreimer 1998; Kreimer 2002), see also Brouder (2000).
(with respect to the Lie bracket given by the first pre-Lie structure), was first investigated in Dür (1986), and intensively studied by Kreimer for renormalization purposes in Quantum Field Theory (Connes and Kreimer 1998; Kreimer 2002), see also Brouder (2000).

 , where
, where  : A ⊗ A → A ⊗ A is the flip , defined by
: A ⊗ A → A ⊗ A is the flip , defined by 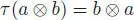 .
.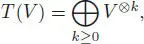
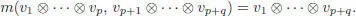
 from T ( V ) to A extending φ .
from T ( V ) to A extending φ .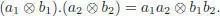
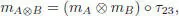
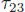 : A ⊗ B ⊗ A ⊗ B → A ⊗ A ⊗ B ⊗ B is defined by the flip of the two middle factors:
: A ⊗ B ⊗ A ⊗ B → A ⊗ A ⊗ B ⊗ B is defined by the flip of the two middle factors: