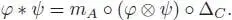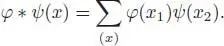
A subspace J ⊂ C is called a subcoalgebra (respectively a left coideal, right coideal and two-sided coideal) of C if Δ( J ) is contained in J ⊗ J (respectively C ⊗ J , J ⊗ C, J ⊗ C + C ⊗ J ) is included in J . The duality alluded to above can be made more precise:
PROPOSITION 1.1.–
1 1) The linear dual C* of a counital coalgebra C is a unital algebra, with product (respectively unit map) the transpose of the coproduct (respectively of the counit).
2 2) Let J be a linear subspace of C. Denote by J⊥ the orthogonal of J in C*.Then:– J is a two-sided coideal if and only if J⊥ is a subalgebra of C*.– J is a left coideal if and only if J⊥ is a left ideal of C*.– J is a right coideal if and only if J⊥ is a right ideal of C*.– J is a subcoalgebra if and only if J⊥ is a two-sided ideal of C*.
PROOF.– For any subspace K of C* , we will denote by K ⊥the subspace of those elements of C on which any element of K vanishes. It coincides with the intersection of the orthogonal of K with C , via the canonical embedding C ↪ C **. Therefore, for any linear subspaces J ⊂ C and K ⊂ C *we have:

Suppose that J is a two-sided coideal. Take any ξ, η in J ⊥. For any x ∈ J , we have:
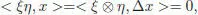
as Δ x ⊂ J ⊗ C + C ⊗ J . Therefore, J ⊥is a subalgebra of C *. Conversely if J ⊥is a subalgebra, then:
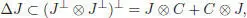
which proves the first assertion. We leave the reader to prove the three other assertions along the same lines. □
Dually, we have the following:
PROPOSITION 1.2.– Let K be a linear subspace of C*. Then :
– K⊥ is a two-sided coideal if and only if K is a subalgebra of C*.
– K⊥ is a left coideal if and only if K is a left ideal of C*.
– K⊥ is a right coideal if and only if K is a right ideal of C*.
– K⊥ is a subcoalgebra if and only if K is a two-sided ideal of C*.
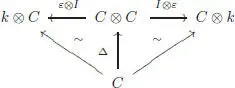
PROOF.– The linear dual ( C ⊗ C ) *naturally contains the tensor product C *⊗ C *. Take as a multiplication the restriction of t Δ to C *⊗ C *:
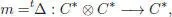
and put u = tε : k → C *. It is easily seen, by just reverting the arrows of the corresponding diagrams, that the coassociativity of Δ implies the associativity of m , and that the counit property for ε implies that u is a unit. □
Note that the duality property is not perfect: if the linear dual of a coalgebra is always an algebra, the linear dual of an algebra is generally not a coalgebra. However, the restricted dual A° of an algebra A is a coalgebra. It is defined as the space of linear forms on A vanishing on some finite-codimensional ideal (Sweedler 1969).
The coalgebra C is cocommutative if 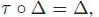 where
where 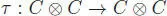 is the flip. It will be convenient to use Sweedler’s notation :
is the flip. It will be convenient to use Sweedler’s notation :
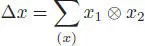
Cocommutativity then expresses as:
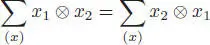
In Sweedler’s notation coassociativity reads as:

We will sometimes write the iterated coproduct as:
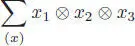
Sometimes, we will even mix the two ways of using Sweedler’s notation for the iterated coproduct, in the case where we want to partially keep track of how we have constructed it (Dǎscǎlescu et al . 2001). For example,
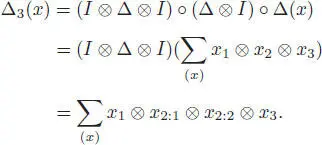
With any vector space V , we can associate its tensor coalgebra Tc ( V ). It is isomorphic to T ( V ) as a vector space. The coproduct is given by the deconcatenation :

The counit is given by the natural projection of Tc ( V ) onto k .
Let C and D be the unital k -coalgebras. We put a counital coalgebra structure on C ⊗ D in the following way: the comultiplication is given by:
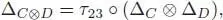
where  is again the flip of the two middle factors, and the counity is given by εC ⊗ D = εC ⊗ εD .
is again the flip of the two middle factors, and the counity is given by εC ⊗ D = εC ⊗ εD .
1.2.3. Convolution product
Let A be an algebra and C be a coalgebra (over the same field k ). Then, there is an associative product on the space 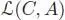 of linear maps from C to A , called the convolution product . It is given by:
of linear maps from C to A , called the convolution product . It is given by:
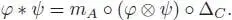
In Sweedler’s notation, it reads:
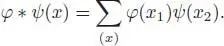
The associativity is a direct consequence of both the associativity of A and coassociativity of C .
Читать дальше



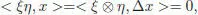
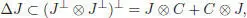
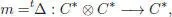
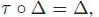 where
where 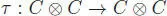 is the flip. It will be convenient to use Sweedler’s notation :
is the flip. It will be convenient to use Sweedler’s notation :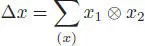
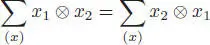

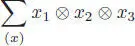
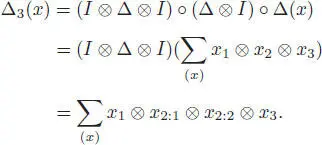

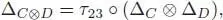
 is again the flip of the two middle factors, and the counity is given by εC ⊗ D = εC ⊗ εD .
is again the flip of the two middle factors, and the counity is given by εC ⊗ D = εC ⊗ εD .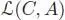 of linear maps from C to A , called the convolution product . It is given by:
of linear maps from C to A , called the convolution product . It is given by: