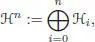with | x (j)| ≥ 1. The grading imposes:
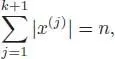
so the maximum possible for any degree | x (j)| is n — k . □
1.3.2. An example: the Hopf algebra of decorated rooted trees
A rooted tree is an oriented graph with a finite number of vertices, one among them being distinguished as the root , such that any vertex admits exactly one outgoing edge, except the root which has no outgoing edges. Here is the list of rooted trees up to five vertices, where the edges are tacitly oriented from top to bottom:

A rooted forest is a finite collection of rooted trees. The Connes-Kreimer Hopf algebra 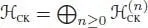 is the Hopf algebra of rooted forests over k , graded by the number of vertices. It is the free commutative algebra on the linear space
is the Hopf algebra of rooted forests over k , graded by the number of vertices. It is the free commutative algebra on the linear space 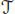 spanned by nonempty rooted trees. The coproduct on a rooted forest u (i.e. a product of rooted trees) is described as follows: the set U of vertices of a forest u is endowed with a partial order defined by x ≤ y if and only if there is a path from a root to y passing through x . Any subset W of the set of vertices U of u defines a subforest w of u in an obvious manner, that is, by keeping the edges of u which link two elements of W . The coproduct is then defined by:
spanned by nonempty rooted trees. The coproduct on a rooted forest u (i.e. a product of rooted trees) is described as follows: the set U of vertices of a forest u is endowed with a partial order defined by x ≤ y if and only if there is a path from a root to y passing through x . Any subset W of the set of vertices U of u defines a subforest w of u in an obvious manner, that is, by keeping the edges of u which link two elements of W . The coproduct is then defined by:
[1.8] 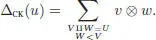
Here, the notation W < V means that y < x for any vertex x of v and any vertex y of w , such that x and y are comparable. Such a couple ( V , W ) is also called an admissible cut , with crown (or pruning) v and trunk w . We have, for example:
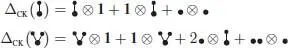
With the restriction that V and W will be nonempty (i.e. if V and W give rise to an ordered partition of U into two blocks), we get the restricted coproduct:
[1.9] 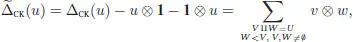
which is often displayed as Σ (u) u ′ ⊗ u ″ in Sweedler’s notation. The iterated restricted coproduct, in terms of ordered partitions of U into n blocks, writes:
[1.10] 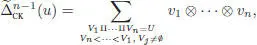
and we get the full-iterated coproduct 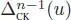 by allowing empty blocks in the formula above. The coassociativity of the coproduct follows immediately.
by allowing empty blocks in the formula above. The coassociativity of the coproduct follows immediately.
Note, however, that the relation < on the subsets of vertices is not transitive. The notation Vn < … < V 1is to be understood as Vi < Vj for any i > j , i , j ∈ {1,…, n }.
1.3.3. Connected filtered bialgebras
A filtered bialgebra on k is a k -vector space together with an increasing ℕ-indexed filtration:
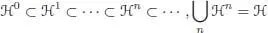
endowed with a product m : ℋ ⊗ ℋ → ℋ, a coproduct Δ : ℋ → ℋ ⊗ ℋ, a unit u : k → ℋ, a counit ε : ℋ → k and an antipode S : ℋ → ℋ, fulfilling the usual axioms of a bialgebra, and such that:
[1.11] 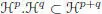
[1.12] 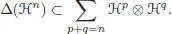
It is easy (and left to the reader) to show that the unit u and the counit ε are of degree zero, if we consider the filtration on the base field k given by k 0= {0} and kn = k for any n ≥ 1. Namely, u ( kn ) ⊂ ℋ nand ε (ℋ n) ⊂ kn for any n ≥ 0.
If we ask for the existence of an antipode S , we get the definition of a filtered Hopf algebra if the antipode is of degree zero, that is, if:
[1.13] 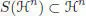
for any n ⊂ 0. Contrarily to the graded case, it is not likely that a filtered bialgebra with antipode is automatically a filtered Hopf algebra (see, for example, Montgomery (1993, Lemma 5.2.8), Andruskiewitsch and Schneider (2002) and Andruskiewitsch and Cuadra (2013)). The antipode is, however, of degree zero in the connected case: for any x ∈ ℋ, we set
[1.14] 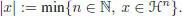
We say that the filtered bialgebra ℋ is connected if ℋ 0is one-dimensional. There is an analogue of Proposition 1.6 in the connected filtered case, the proof of which is very similar:
PROPOSITION 1.7.– For any x ∈ ℋ n, n ≥ 1, we can write :
[1.15] 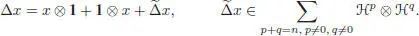
The map 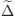 is coassociative on Ker ε and
is coassociative on Ker ε and 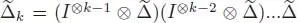 sends ℋ ninto (ℋ n-k) ⊗k + 1.
sends ℋ ninto (ℋ n-k) ⊗k + 1.
As an easy corollary, the degree of the antipode is also zero in the connected case, that is, S (ℋ n) ⊆ ℋ nfor any n . This is an immediate consequence of the recursive formulae [1.19]and [1.20]below.
Any graded bialgebra, or the Hopf algebra, is obviously filtered by the canonical filtration associated with the grading:
[1.16] 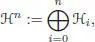
Читать дальше

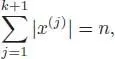

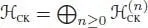 is the Hopf algebra of rooted forests over k , graded by the number of vertices. It is the free commutative algebra on the linear space
is the Hopf algebra of rooted forests over k , graded by the number of vertices. It is the free commutative algebra on the linear space  spanned by nonempty rooted trees. The coproduct on a rooted forest u (i.e. a product of rooted trees) is described as follows: the set U of vertices of a forest u is endowed with a partial order defined by x ≤ y if and only if there is a path from a root to y passing through x . Any subset W of the set of vertices U of u defines a subforest w of u in an obvious manner, that is, by keeping the edges of u which link two elements of W . The coproduct is then defined by:
spanned by nonempty rooted trees. The coproduct on a rooted forest u (i.e. a product of rooted trees) is described as follows: the set U of vertices of a forest u is endowed with a partial order defined by x ≤ y if and only if there is a path from a root to y passing through x . Any subset W of the set of vertices U of u defines a subforest w of u in an obvious manner, that is, by keeping the edges of u which link two elements of W . The coproduct is then defined by:
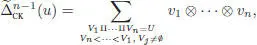
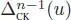 by allowing empty blocks in the formula above. The coassociativity of the coproduct follows immediately.
by allowing empty blocks in the formula above. The coassociativity of the coproduct follows immediately.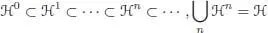
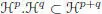
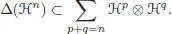
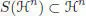
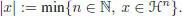
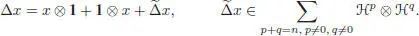
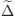 is coassociative on Ker ε and
is coassociative on Ker ε and 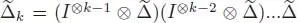 sends ℋ ninto (ℋ n-k) ⊗k + 1.
sends ℋ ninto (ℋ n-k) ⊗k + 1.