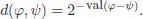and in that case, if x is a homogeneous element, x is of degree n if and only if | x | = n .
1.3.4. The convolution product
An important result is that any connected filtered bialgebra is indeed a filtered Hopf algebra, in the sense that the antipode comes for free. We give a proof of this fact as well as a recursive formula for the antipode using the convolution product : let ℋ be a (connected filtered) bialgebra, and let  be any k -algebra (which will be called the target algebra ): the convolution product on
be any k -algebra (which will be called the target algebra ): the convolution product on 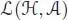 is given by:
is given by:
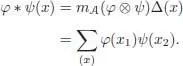
PROPOSITION 1.8.– The map 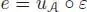 , given by
, given by 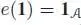 and e ( x ) = 0 for any x ∈ Ker ε, is a unit for the convolution product. Moreover, the set
and e ( x ) = 0 for any x ∈ Ker ε, is a unit for the convolution product. Moreover, the set 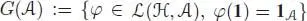 endowed with the convolution product is a group .
endowed with the convolution product is a group .
PROOF.– The first statement is straightforward. To prove the second, let us consider the formal series:
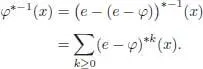
Using ( e — φ )( 1) = 0, we have ( e — φ ) *k( 1) = 0 immediately, and for any x ∈ Ker ε :
[1.17] 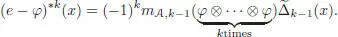
When x ∈ ℋ n, this expression vanishes and then for k ≥ n + 1. The formal series then ends up with a finite number of terms for any x , which proves the result. □
COROLLARY 1.1.– Any connected filtered bialgebra ℋ is a filtered Hopf algebra. The antipode is defined by :
[1.18] 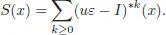
It is given by S ( 1) = 1 and recursively by any of the two formulae for x ∈ Ker ε :
[1.19] 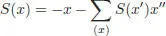
[1.20] 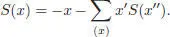
PROOF.– The antipode, when it exists, is the inverse of the identity for the convolution product on 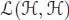 . We then just need to apply Proposition 1.8 with
. We then just need to apply Proposition 1.8 with 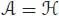 . The two recursive formulas come directly from the two equalities:
. The two recursive formulas come directly from the two equalities:
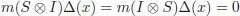
fulfilled by any x ∈ Ker ε .
Let 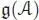 be the subspace of
be the subspace of 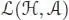 formed by the elements α , such that α ( 1) = 0. It is clearly a subalgebra of
formed by the elements α , such that α ( 1) = 0. It is clearly a subalgebra of 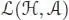 for the convolution product. We have:
for the convolution product. We have:
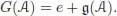
From now on, we will suppose that the ground field k is of characteristic zero. For any x ∈ ℋ n, the exponential:
[1.21] 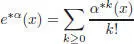
is a finite sum (ending up at k = n ). It is a bijection from 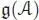 onto
onto 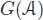 . Its inverse is given by:
. Its inverse is given by:
[1.22] 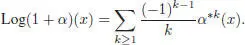
This sum again ends up at k = n for any x ∈ ℋ n. Let us introduce a decreasing filtration on 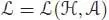 :
:
[1.23] 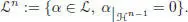
Clearly, 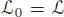 and
and 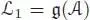 . We define the valuation val φ of an element φ of
. We define the valuation val φ of an element φ of 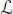 as the greatest integer k , such that φ is in
as the greatest integer k , such that φ is in 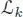 . In the sequel we will consider the ultrametric distance on
. In the sequel we will consider the ultrametric distance on 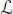 induced by the filtration:
induced by the filtration:
[1.24] 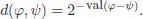
Читать дальше

 be any k -algebra (which will be called the target algebra ): the convolution product on
be any k -algebra (which will be called the target algebra ): the convolution product on 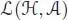 is given by:
is given by: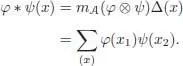
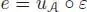 , given by
, given by 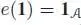 and e ( x ) = 0 for any x ∈ Ker ε, is a unit for the convolution product. Moreover, the set
and e ( x ) = 0 for any x ∈ Ker ε, is a unit for the convolution product. Moreover, the set 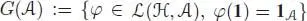 endowed with the convolution product is a group .
endowed with the convolution product is a group .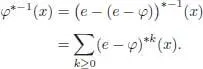
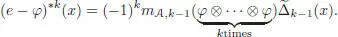
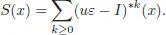
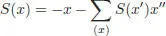
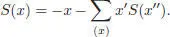
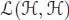 . We then just need to apply Proposition 1.8 with
. We then just need to apply Proposition 1.8 with 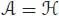 . The two recursive formulas come directly from the two equalities:
. The two recursive formulas come directly from the two equalities: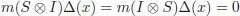
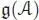 be the subspace of
be the subspace of 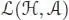 formed by the elements α , such that α ( 1) = 0. It is clearly a subalgebra of
formed by the elements α , such that α ( 1) = 0. It is clearly a subalgebra of 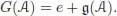
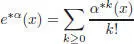
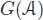 . Its inverse is given by:
. Its inverse is given by: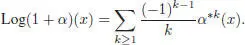
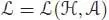 :
: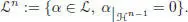
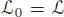 and
and 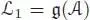 . We define the valuation val φ of an element φ of
. We define the valuation val φ of an element φ of 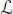 as the greatest integer k , such that φ is in
as the greatest integer k , such that φ is in 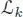 . In the sequel we will consider the ultrametric distance on
. In the sequel we will consider the ultrametric distance on