1 ...6 7 8 10 11 12 ...24 For any 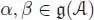 let [ α, β ] = α * β — β * α .
let [ α, β ] = α * β — β * α .
PROPOSITION 1.9.– We have the inclusion :
[1.25] 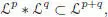
and moreover, the metric space endowed with the distance defined by [1.24] is complete .
PROOF.– Take any x ∈ ℋ p+q − 1, and any 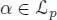 and
and 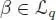 . We have:
. We have:
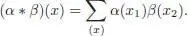
Recall that we denote by | x | the minimal n , such that x ∈ ℋ n. Since | x 1| + | x 2| = | x | ≤ p + q — 1, either | x 1| ≤ p – 1 or | x 2| ≤ q — 1, so the expression vanishes. Now, if ( ψn ) is a Cauchy sequence in 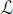 , it is seen immediately that this sequence is locally stationary , that is, for any x ∈ ℋ there exists N ( x ) ∈ ℕ, such that ψn ( x ) = ψ N (x)( x ) for any n ≥ N ( x ). Then, the limit of ( ψn ) exists and is clearly defined by:
, it is seen immediately that this sequence is locally stationary , that is, for any x ∈ ℋ there exists N ( x ) ∈ ℕ, such that ψn ( x ) = ψ N (x)( x ) for any n ≥ N ( x ). Then, the limit of ( ψn ) exists and is clearly defined by:
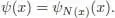
□
As a corollary, the Lie algebra 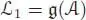 is pro-nilpotent , in a sense that it is the projective limit of the Lie algebras
is pro-nilpotent , in a sense that it is the projective limit of the Lie algebras 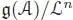 , which are nilpotent.
, which are nilpotent.
Let ℋ be a connected filtered Hopf algebra over k , and let A be a k -algebra. We will consider unital algebra morphisms from ℋ to the target algebra  . When the algebra
. When the algebra  is commutative, we will call them, slightly abusively, characters . We recover, of course, the usual notion of character when the algebra
is commutative, we will call them, slightly abusively, characters . We recover, of course, the usual notion of character when the algebra  is the ground field k .
is the ground field k .
The notion of character involves only the algebra structure of ℋ. On the contrary, the convolution product on 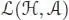 involves only the coalgebra structure on ℋ. Let us now consider the full Hopf algebra structure on ℋ and see what happens to algebra morphisms with the convolution product:
involves only the coalgebra structure on ℋ. Let us now consider the full Hopf algebra structure on ℋ and see what happens to algebra morphisms with the convolution product:
PROPOSITION 1.10.– Let ℋ be any Hopf algebra over k, and let be a commutative k-algebra. Then, the characters from ℋ to form a group under the convolution product, and for any , the inverse is given by :
[1.26] 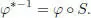
PROOF.– Using the fact that Δ is an algebra morphism, we have for any x, y ∈ ℋ:
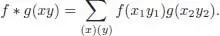
If  is commutative and if f and g are characters, we get:
is commutative and if f and g are characters, we get:
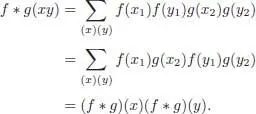
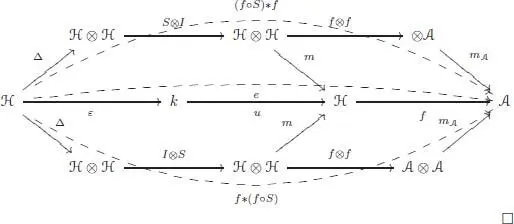
The unit 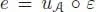 is an algebra morphism. The formula for the inverse of a character comes easily from the commutativity of the following diagram:
is an algebra morphism. The formula for the inverse of a character comes easily from the commutativity of the following diagram:
We call infinitesimal characters with values in the algebra those elements α of  , such that:
, such that:
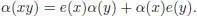
PROPOSITION 1.11.– Let ℋ be a connected filtered Hopf algebra, and suppose that is a commutative algebra. Let (respectively ) be the set of characters of ℋ with values in (respectively the set of infinitesimal characters of ℋ with values in ). Then, is a subgroup of G, the exponential restricts to a bijection from onto , and is a Lie subalgebra of .
PROOF.– Take two infinitesimal characters α and β with values in  and compute:
and compute:
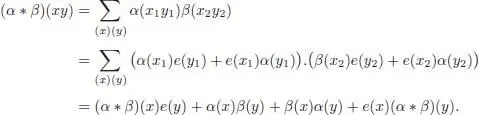
Using the commutativity of  , we immediately get:
, we immediately get:
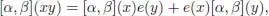
which shows that 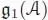 is a Lie algebra. Now, for
is a Lie algebra. Now, for 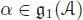 , we have:
, we have:
Читать дальше

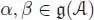 let [ α, β ] = α * β — β * α .
let [ α, β ] = α * β — β * α .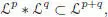
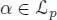 and
and 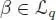 . We have:
. We have: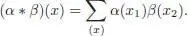
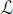 , it is seen immediately that this sequence is locally stationary , that is, for any x ∈ ℋ there exists N ( x ) ∈ ℕ, such that ψn ( x ) = ψ N (x)( x ) for any n ≥ N ( x ). Then, the limit of ( ψn ) exists and is clearly defined by:
, it is seen immediately that this sequence is locally stationary , that is, for any x ∈ ℋ there exists N ( x ) ∈ ℕ, such that ψn ( x ) = ψ N (x)( x ) for any n ≥ N ( x ). Then, the limit of ( ψn ) exists and is clearly defined by: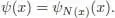
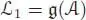 is pro-nilpotent , in a sense that it is the projective limit of the Lie algebras
is pro-nilpotent , in a sense that it is the projective limit of the Lie algebras 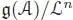 , which are nilpotent.
, which are nilpotent. . When the algebra
. When the algebra 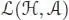 involves only the coalgebra structure on ℋ. Let us now consider the full Hopf algebra structure on ℋ and see what happens to algebra morphisms with the convolution product:
involves only the coalgebra structure on ℋ. Let us now consider the full Hopf algebra structure on ℋ and see what happens to algebra morphisms with the convolution product: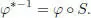
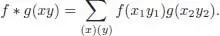
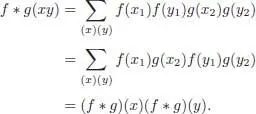
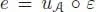 is an algebra morphism. The formula for the inverse of a character comes easily from the commutativity of the following diagram:
is an algebra morphism. The formula for the inverse of a character comes easily from the commutativity of the following diagram:
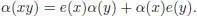
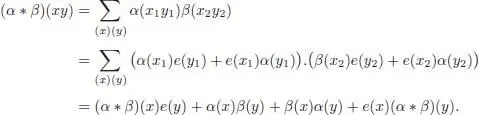
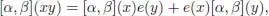
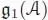 is a Lie algebra. Now, for
is a Lie algebra. Now, for 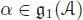 , we have:
, we have:










