1 ...7 8 9 11 12 13 ...24 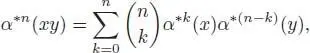
as easily seen by induction on n . A straightforward computation then yields:
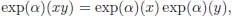
with
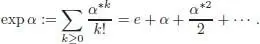
The series above makes sense thanks to connectedness, as explained in section 1.3.4. Now let 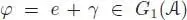 , and let
, and let 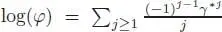 . Set φ*t := exp( t log φ ) for t ∈ k . It coincides with the n thconvolution power of φ for any integer n . Hence, φ *tis an
. Set φ*t := exp( t log φ ) for t ∈ k . It coincides with the n thconvolution power of φ for any integer n . Hence, φ *tis an  -valued character of ℋ for any t ∈ k . Indeed, for any x, y ∈ ℋ, the expression φ *t( xy ) – φ *t( x ) φ *t( y ) is polynomial in t and vanishes on all integers, and hence, vanishes identically. Differentiating with respect to t at t = 0, we immediately find that log φ is an infinitesimal character. □
-valued character of ℋ for any t ∈ k . Indeed, for any x, y ∈ ℋ, the expression φ *t( xy ) – φ *t( x ) φ *t( y ) is polynomial in t and vanishes on all integers, and hence, vanishes identically. Differentiating with respect to t at t = 0, we immediately find that log φ is an infinitesimal character. □
1.3.6. Group schemes and the Cartier-Milnor-Moore-Quillen theorem
THEOREM 1.1 (Cartier, Milnor, Moore, Quillen).– Let be a cocommutative connected filtered Hopf algebra and let be the Lie algebra of its primitive elements, endowed with the filtration induced by the one of 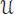 , which in turns induces a filtration on the enveloping algebra
, which in turns induces a filtration on the enveloping algebra 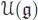 . Then ,
. Then ,  and
and 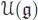 are the isomorphic as filtered Hopf algebras. If
are the isomorphic as filtered Hopf algebras. If 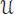 is graded, then the two Hopf algebras are isomorphic as graded Hopf algebras .
is graded, then the two Hopf algebras are isomorphic as graded Hopf algebras .
PROOF.– The following proof is borrowed from Foissy’s thesis. The embedding 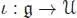 obviously induces an algebra morphism
obviously induces an algebra morphism
[1.27] 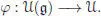
It is easy to show that φ is also a coalgebra morphism. It remains to show that φ is surjective, injective and respects the filtrations. Let us first prove the surjectivity by induction on the coradical filtration degree:
[1.28] 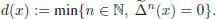
Set 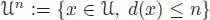 , and similarly for
, and similarly for 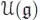 . We can limit ourselves to the kernel of the counit. Any
. We can limit ourselves to the kernel of the counit. Any 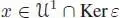 is primitive, hence
is primitive, hence  is obviously a linear isomorphism. Now, for
is obviously a linear isomorphism. Now, for 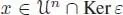 (for some integer n ≥ 2), we can write, using cocommutativity:
(for some integer n ≥ 2), we can write, using cocommutativity:
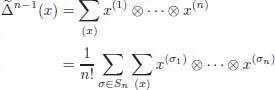
where the x (j)s are of coradical filtration degree 1, hence primitive. But, we also have:
[1.29] 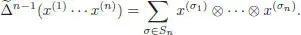
Hence, the element 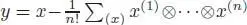 belongs to
belongs to 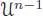 . It is a linear combination of products of primitive elements by induction hypothesis, hence so is x . We have thus proven that
. It is a linear combination of products of primitive elements by induction hypothesis, hence so is x . We have thus proven that 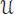 is generated by
is generated by  , which amounts to the surjectivity of φ .
, which amounts to the surjectivity of φ .
Now consider a nonzero element 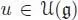 , such that φ ( u ) = 0, and such that d ( u ) is minimal. We have already proven d ( u ) ≥ 2. We now compute:
, such that φ ( u ) = 0, and such that d ( u ) is minimal. We have already proven d ( u ) ≥ 2. We now compute:
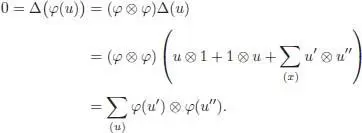
By minimality hypothesis on d ( u ), we then get Σ (u) u ′ ⊗ u ″ = 0. Hence, u is primitive, that is, d ( u ) = 1, a contradiction. Hence, φ is injective. The compatibility with the original filtration or graduation is obvious. □
Now, let ℋ : ∪ n ≥ 0ℋ nbe a connected filtered Hopf algebra and let  be a commutative unital algebra. We suppose that the components of the filtration are finite-dimensional. The group
be a commutative unital algebra. We suppose that the components of the filtration are finite-dimensional. The group 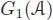 defined in the previous section depends functorially on the target algebra
defined in the previous section depends functorially on the target algebra  : in particular, when the Hopf algebra ℋ itself is commutative, the correspondence
: in particular, when the Hopf algebra ℋ itself is commutative, the correspondence 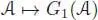 is a group scheme . In the graded case with finite-dimensional components, it is possible to reconstruct the Hopf algebra ℋ from the group scheme. We have indeed:
is a group scheme . In the graded case with finite-dimensional components, it is possible to reconstruct the Hopf algebra ℋ from the group scheme. We have indeed:
Читать дальше

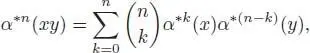
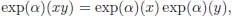
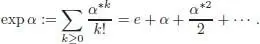
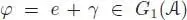 , and let
, and let 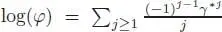 . Set φ*t := exp( t log φ ) for t ∈ k . It coincides with the n thconvolution power of φ for any integer n . Hence, φ *tis an
. Set φ*t := exp( t log φ ) for t ∈ k . It coincides with the n thconvolution power of φ for any integer n . Hence, φ *tis an  -valued character of ℋ for any t ∈ k . Indeed, for any x, y ∈ ℋ, the expression φ *t( xy ) – φ *t( x ) φ *t( y ) is polynomial in t and vanishes on all integers, and hence, vanishes identically. Differentiating with respect to t at t = 0, we immediately find that log φ is an infinitesimal character. □
-valued character of ℋ for any t ∈ k . Indeed, for any x, y ∈ ℋ, the expression φ *t( xy ) – φ *t( x ) φ *t( y ) is polynomial in t and vanishes on all integers, and hence, vanishes identically. Differentiating with respect to t at t = 0, we immediately find that log φ is an infinitesimal character. □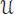 , which in turns induces a filtration on the enveloping algebra
, which in turns induces a filtration on the enveloping algebra 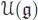 . Then ,
. Then , 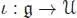 obviously induces an algebra morphism
obviously induces an algebra morphism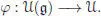
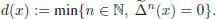
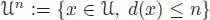 , and similarly for
, and similarly for 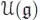 . We can limit ourselves to the kernel of the counit. Any
. We can limit ourselves to the kernel of the counit. Any 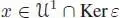 is primitive, hence
is primitive, hence  is obviously a linear isomorphism. Now, for
is obviously a linear isomorphism. Now, for 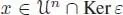 (for some integer n ≥ 2), we can write, using cocommutativity:
(for some integer n ≥ 2), we can write, using cocommutativity: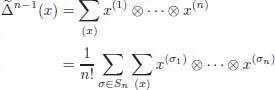
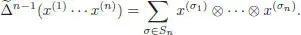
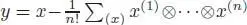 belongs to
belongs to 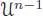 . It is a linear combination of products of primitive elements by induction hypothesis, hence so is x . We have thus proven that
. It is a linear combination of products of primitive elements by induction hypothesis, hence so is x . We have thus proven that  , which amounts to the surjectivity of φ .
, which amounts to the surjectivity of φ .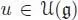 , such that φ ( u ) = 0, and such that d ( u ) is minimal. We have already proven d ( u ) ≥ 2. We now compute:
, such that φ ( u ) = 0, and such that d ( u ) is minimal. We have already proven d ( u ) ≥ 2. We now compute: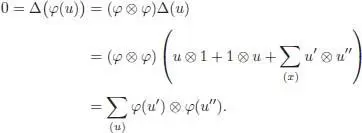
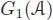 defined in the previous section depends functorially on the target algebra
defined in the previous section depends functorially on the target algebra 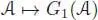 is a group scheme . In the graded case with finite-dimensional components, it is possible to reconstruct the Hopf algebra ℋ from the group scheme. We have indeed:
is a group scheme . In the graded case with finite-dimensional components, it is possible to reconstruct the Hopf algebra ℋ from the group scheme. We have indeed:










