then endows A with a structure of a pro-unipotent group. An example of this situation is given by A = hB [[ h ]], where B is any pre-Lie algebra, and Aj = hjB [[ h ]]. This group admits a more transparent presentation as follows: introduce a fictitious unit 1, such that 1⊳ a = a ⊳ 1= a for any a ∈ A , and define W : A → A by:
[1.45] 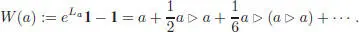
The application W is clearly a bijection. The inverse, denoted by Ω, also appears under the name “pre-Lie Magnus expansion” in Ebrahimi-Fard and Manchon (2009b). It verifies the equation:
[1.46] 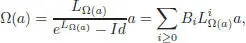
where the Bi s are the Bernoulli numbers. The first few terms are:
[1.47] 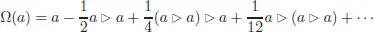
By transferring the BCH product by means of the map W , namely:
[1.48] 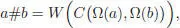
we have W ( a ) # W ( b ) = W ( C ( a , b )) = eLa e Lb 1– 1, hence W ( a )# W ( b ) = W ( a ) + eLa W ( b ). The product # is thus given by the simple formula:
[1.49] 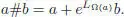
The inverse is given by a #–1= W (–Ω( a )) = e –LΩ(a) 1– 1. If ( A , ⊳) and ( B , ⊳) are two such pre-Lie algebras and ψ : A → B is a filtration-preserving pre-Lie algebra morphism, we should immediately check that for any a , b ∈ A we have:
[1.50] 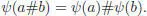
In other words, the group of formal flows is a functor from the category of complete filtered pre-Lie algebras to the category of groups.
When the pre-Lie product ⊳ is associative, all of this simplifies to:
[1.51] 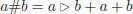
and
[1.52] 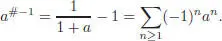
1.4.3. The pre-Lie Poincaré–Birkhoff–Witt theorem
This section exposes a result by Guin and Oudom (2005).
THEOREM 1.3.– Let A be any left pre-Lie algebra, and let S ( A ) be its symmetric algebra, that is, the free commutative algebra on A. Let A Lie be the underlying Lie algebra of A, that is, the vector space A endowed with the Lie bracket given by [ a, b ] = a ⊳ b − b ⊳ a for any a, b ∈ A, and let be the enveloping algebra of A Lie, endowed with its usual increasing filtration. Let us consider the associative algebra as a left module over itself .
There exists a left -module structure on S ( A ) and a canonical left -module isomorphism , such that the associated graded linear map Gr is an isomorphism of commutative graded algebras .
PROOF.– The Lie algebra morphism
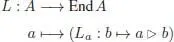
extends by the Leibniz rule to a unique Lie algebra morphism L : A → Der S ( A ). Now we claim that the map M : A → End S ( A ) defined by:
[1.53] 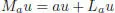
is a Lie algebra morphism. Indeed, for any a, b ∈ A and u ∈ S ( A ) we have:
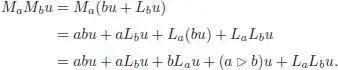
Hence

which proves the claim. Now M extends, by universal property of the enveloping algebra, to a unique algebra morphism 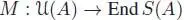 . The linear map:
. The linear map:

is clearly a morphism of left 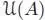 -modules. It is immediately seen by induction that for any a 1,…, an ∈ A , we have η ( a 1… an ) = a 1… an + v , where v is a sum of terms of degree < n – 1. This proves the theorem. □
-modules. It is immediately seen by induction that for any a 1,…, an ∈ A , we have η ( a 1… an ) = a 1… an + v , where v is a sum of terms of degree < n – 1. This proves the theorem. □
REMARK 1.3.– Let us recall that the symmetrization map 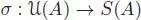 , uniquely determined by σ ( an ) = an for any a ∈ A and any integer n, is an isomorphism for the two A Lie- module structures given by the adjoint action. This is not the case for the map η defined above. The fact that it is possible to replace the adjoint action of on itself by the simple left multiplication is a remarkable property ofpre-Lie algebras, and makes Theorem 1.3 different from the usual Lie algebra PBW theorem .
, uniquely determined by σ ( an ) = an for any a ∈ A and any integer n, is an isomorphism for the two A Lie- module structures given by the adjoint action. This is not the case for the map η defined above. The fact that it is possible to replace the adjoint action of on itself by the simple left multiplication is a remarkable property ofpre-Lie algebras, and makes Theorem 1.3 different from the usual Lie algebra PBW theorem .
Let us finally note that, if p stands for the projection from S ( A ) onto A , for any a 1,…, ak ∈ A , we easily get:
[1.54] 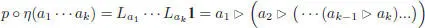
by a simple induction on k . The linear isomorphism η transfers the product of the enveloping algebra 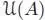 into a noncommutative product * on
into a noncommutative product * on 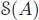 defined by:
defined by:
Читать дальше

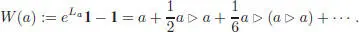
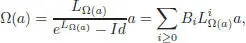
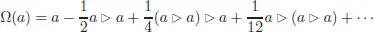
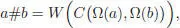
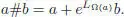
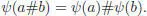
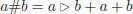
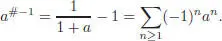
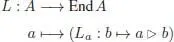
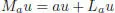
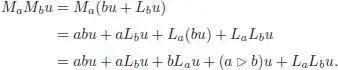

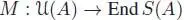 . The linear map:
. The linear map:
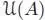 -modules. It is immediately seen by induction that for any a 1,…, an ∈ A , we have η ( a 1… an ) = a 1… an + v , where v is a sum of terms of degree < n – 1. This proves the theorem. □
-modules. It is immediately seen by induction that for any a 1,…, an ∈ A , we have η ( a 1… an ) = a 1… an + v , where v is a sum of terms of degree < n – 1. This proves the theorem. □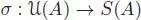 , uniquely determined by σ ( an ) = an for any a ∈ A and any integer n, is an isomorphism for the two A Lie- module structures given by the adjoint action. This is not the case for the map η defined above. The fact that it is possible to replace the adjoint action of on itself by the simple left multiplication is a remarkable property ofpre-Lie algebras, and makes Theorem 1.3 different from the usual Lie algebra PBW theorem .
, uniquely determined by σ ( an ) = an for any a ∈ A and any integer n, is an isomorphism for the two A Lie- module structures given by the adjoint action. This is not the case for the map η defined above. The fact that it is possible to replace the adjoint action of on itself by the simple left multiplication is a remarkable property ofpre-Lie algebras, and makes Theorem 1.3 different from the usual Lie algebra PBW theorem .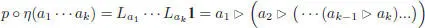
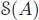 defined by:
defined by:










