[1.67] 
and finally, the following equivariance property is satisfied :
[1.68] 
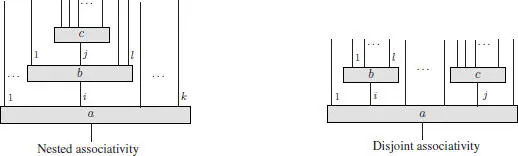
where is definedby letting permute the set Ei = { i , i + 1,…, i + l – 1} of cardinality l, and then by letting σ permute the set {1,…, i – 1, Ei , i + l ,…, k + l – 1} of cardinality k .
The two associativity properties are graphically represented as follows:
1.5.3. A definition for linear operads
We are now ready to give the precise definition of a linear operad:
DEFINITION 1.1.– An operad (in the symmetric monoidal category of k-vector spaces) is given by a collection of vector spaces 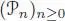 , a right action of the symmetric group Sn on
, a right action of the symmetric group Sn on  , a distinguished element
, a distinguished element 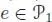 and a collection of partial compositions :
and a collection of partial compositions :
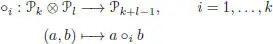
subject to the associativity, unit and equivariance axioms of Proposition 1.13 .
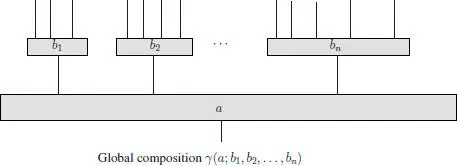
The global composition is defined by:
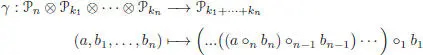
and is graphically represented as follows:
The operad 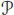 is augmented if
is augmented if  and
and 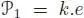 . For any operad
. For any operad 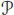 , a
, a 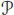 -algebra structure on the vector space V is a morphism of operads from
-algebra structure on the vector space V is a morphism of operads from 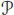 to Endop( V ). For any two
to Endop( V ). For any two 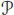 -algebras V and W , a morphism of
-algebras V and W , a morphism of 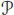 -algebras is a linear map f : V → W , such that for any n ≥ 0 and for any
-algebras is a linear map f : V → W , such that for any n ≥ 0 and for any 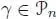 , the following diagram commutes,
, the following diagram commutes,
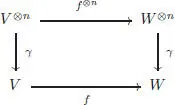
where we have denoted by the same letter γ the element of 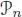 and its images in Endop( V ) nand Endop( W ) n.
and its images in Endop( V ) nand Endop( W ) n.
Now let V be any k -vector space. The free -algebra is a 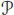 -algebra
-algebra 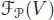 endowed with a linear map
endowed with a linear map 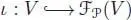 , such that for any
, such that for any 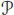 -algebra A and for any linear map f : V → A , there is a unique
-algebra A and for any linear map f : V → A , there is a unique 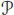 -algebra morphism
-algebra morphism 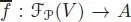 , such that
, such that 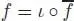 . The free
. The free 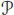 -algebra
-algebra 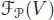 is unique up to isomorphism, and we can prove that a concrete presentation of it is given by:
is unique up to isomorphism, and we can prove that a concrete presentation of it is given by:
[1.69] 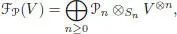
with the map ι being obviously defined. When V is of finite dimension d , the corresponding free 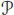 -algebra is often called the free -algebra with d generators .
-algebra is often called the free -algebra with d generators .
There are several other equivalent definitions for an operad. For more details about operads, see, for example, Loday (1996) and Loday and Vallette (2012).
1.5.4. A few examples of operads
1.5.4.1. The operad ASSOC
This operad governs associative algebras. ASSOC nis given by k [ Sn ] (the algebra of the symmetric group Sn ) for any n ≥ 0, whereas ASSOC 0:= {0}. The right action of Sn on ASSOC nis given by linear extension of right multiplication:
[1.70] 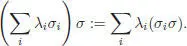
Let σ ∈ ASSOC kand 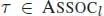 . The partial compositions are given for any i = 1,…, k by:
. The partial compositions are given for any i = 1,…, k by:
Читать дальше




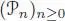 , a right action of the symmetric group Sn on
, a right action of the symmetric group Sn on  , a distinguished element
, a distinguished element 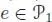 and a collection of partial compositions :
and a collection of partial compositions :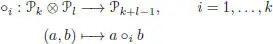
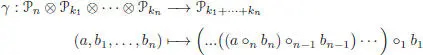

 is augmented if
is augmented if  and
and 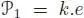 . For any operad
. For any operad 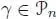 , the following diagram commutes,
, the following diagram commutes,
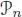 and its images in Endop( V ) nand Endop( W ) n.
and its images in Endop( V ) nand Endop( W ) n.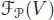 endowed with a linear map
endowed with a linear map 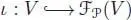 , such that for any
, such that for any 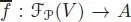 , such that
, such that 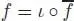 . The free
. The free 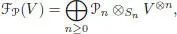
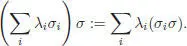
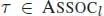 . The partial compositions are given for any i = 1,…, k by:
. The partial compositions are given for any i = 1,…, k by:










