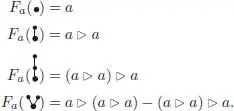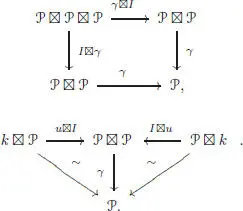
These two diagrams commute if and only if e verifies the unit axiom and the partial compositions verify the two associativity axioms and the equivariance axiom (Loday and Vallette 2012).
1.6. Pre-Lie algebras (continued)
1.6.1. Pre-Lie algebras and augmented operads
1.6.1.1. General construction
We adopt the notations of section 1.5. The sum of the partial compositions yields a right pre-Lie algebra structure on the free 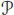 -algebra with one generator, more precisely on
-algebra with one generator, more precisely on 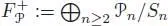 , namely:
, namely:
[1.77] 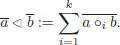
Following Chapoton (2002), we can consider the pro-unipotent group 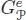 associated with the completion of the pre-Lie algebra
associated with the completion of the pre-Lie algebra 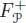 for the filtration induced by the grading. More precisely, Chapoton’s group
for the filtration induced by the grading. More precisely, Chapoton’s group 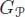 is given by the elements
is given by the elements 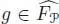 , such that g 1≠ 0, whereas
, such that g 1≠ 0, whereas 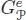 is the subgroup of
is the subgroup of 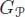 formed by elements g , such that g 1= e .
formed by elements g , such that g 1= e .
Any element 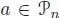 gives rise to an n -ary operation
gives rise to an n -ary operation 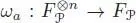 , and for any
, and for any 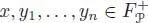 , we have 1 (Manchon and Saidi 2011):
, we have 1 (Manchon and Saidi 2011):
[1.78] 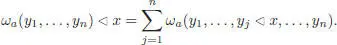
1.6.1.2. The pre-Lie operad
Pre-Lie algebras are algebras over the pre-Lie operad , which has been described in detail by Chapoton and Livernet (2001) as follows: 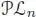 is the vector space of labeled rooted trees, and the partial composition s ∘ i t is given by summing all of the possible ways of inserting the tree t inside the tree s at the vertex labeled by i . To be precise, the sum runs over the possible ways of branching on t the edges of s , which arrive on the vertex i .
is the vector space of labeled rooted trees, and the partial composition s ∘ i t is given by summing all of the possible ways of inserting the tree t inside the tree s at the vertex labeled by i . To be precise, the sum runs over the possible ways of branching on t the edges of s , which arrive on the vertex i .
The free left pre-Lie algebra with one generator is then given by the space  of rooted trees, as quotienting with the symmetric group actions amounts to neglect the labels. The pre-Lie operation ( s,t ) ↦ ( s → t ) is given by the sum of the graftings of s on t at all vertices of t . As a result of [1.78], we have two pre-Lie operations on
of rooted trees, as quotienting with the symmetric group actions amounts to neglect the labels. The pre-Lie operation ( s,t ) ↦ ( s → t ) is given by the sum of the graftings of s on t at all vertices of t . As a result of [1.78], we have two pre-Lie operations on  , which interact as follows (Manchon and Saidi 2011):
, which interact as follows (Manchon and Saidi 2011):
[1.79] 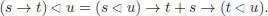
The first pre-Lie operation ⊲ comes from the fact that 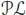 is an augmented operad, whereas the second pre-Lie operation → comes from the fact that
is an augmented operad, whereas the second pre-Lie operation → comes from the fact that 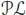 is the pre-Lie operad itself! Similarly:
is the pre-Lie operad itself! Similarly:
THEOREM 1.4.– The free pre-Lie algebra with d generators is the vector space of rooted trees with d colors, endowed with grafting .
1.6.2. A pedestrian approach to free pre-Lie algebra
In this section we give a direct proof of Theorem 1.4 without using operads. It is similar to the proof of the main theorem in Chapoton and Livernet (2001) about the structure of the pre-Lie operad, except that we consider unlabeled trees. We stick to d = 1 (i.e. one generator), the proof for several generators being completely analogous. Let 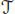 be the vector space spanned by rooted trees. First, the grafting operation is pre-Lie, because for any trees s, t and u in
be the vector space spanned by rooted trees. First, the grafting operation is pre-Lie, because for any trees s, t and u in 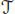 , the expression:
, the expression:
[1.80] 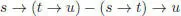
is obtained by summing up all of the possibilities of grafting s and t at some vertex of u . As such, it is obviously symmetric in s and t . Now let ( A , ⊳) be any left pre-lie algebra, and choose any a ∈ A . In order to prove Theorem 1.4 for one generator, we have to show that there is a unique pre-Lie algebra morphism 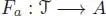 , such that Fa (•) = a . For the first trees, we easily obtain:
, such that Fa (•) = a . For the first trees, we easily obtain:
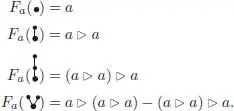
Can we continue like this? We proceed by double induction, first, on the number of vertices, second, on the number of branches, that is, the valence of the root. Write any tree t with n vertices as t = B +( t 1,…, tk ), where the tj s are the branches and B +is the operator that grafts the branches on a common extra root. By the induction hypothesis on n , the images Fa ( tj ) are well-defined.
Читать дальше


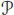 -algebra with one generator, more precisely on
-algebra with one generator, more precisely on 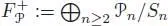 , namely:
, namely: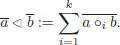
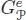 associated with the completion of the pre-Lie algebra
associated with the completion of the pre-Lie algebra 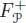 for the filtration induced by the grading. More precisely, Chapoton’s group
for the filtration induced by the grading. More precisely, Chapoton’s group 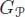 is given by the elements
is given by the elements 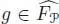 , such that g 1≠ 0, whereas
, such that g 1≠ 0, whereas 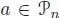 gives rise to an n -ary operation
gives rise to an n -ary operation 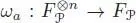 , and for any
, and for any 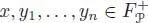 , we have 1 (Manchon and Saidi 2011):
, we have 1 (Manchon and Saidi 2011):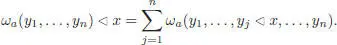
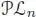 is the vector space of labeled rooted trees, and the partial composition s ∘ i t is given by summing all of the possible ways of inserting the tree t inside the tree s at the vertex labeled by i . To be precise, the sum runs over the possible ways of branching on t the edges of s , which arrive on the vertex i .
is the vector space of labeled rooted trees, and the partial composition s ∘ i t is given by summing all of the possible ways of inserting the tree t inside the tree s at the vertex labeled by i . To be precise, the sum runs over the possible ways of branching on t the edges of s , which arrive on the vertex i . of rooted trees, as quotienting with the symmetric group actions amounts to neglect the labels. The pre-Lie operation ( s,t ) ↦ ( s → t ) is given by the sum of the graftings of s on t at all vertices of t . As a result of [1.78], we have two pre-Lie operations on
of rooted trees, as quotienting with the symmetric group actions amounts to neglect the labels. The pre-Lie operation ( s,t ) ↦ ( s → t ) is given by the sum of the graftings of s on t at all vertices of t . As a result of [1.78], we have two pre-Lie operations on  , which interact as follows (Manchon and Saidi 2011):
, which interact as follows (Manchon and Saidi 2011):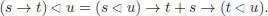
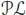 is an augmented operad, whereas the second pre-Lie operation → comes from the fact that
is an augmented operad, whereas the second pre-Lie operation → comes from the fact that 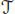 be the vector space spanned by rooted trees. First, the grafting operation is pre-Lie, because for any trees s, t and u in
be the vector space spanned by rooted trees. First, the grafting operation is pre-Lie, because for any trees s, t and u in 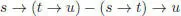
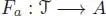 , such that Fa (•) = a . For the first trees, we easily obtain:
, such that Fa (•) = a . For the first trees, we easily obtain: