[1.71] 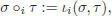
with the notations of equation [1.68]. The reader is invited to check the two associativity axioms, as well as the equivariance axiom which reads:
[1.72] 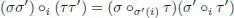
for any σ , σ ′ ∈ ASSOC kand 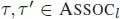 . Let us denote by ek the unit element in the symmetric group Sk . We obviously have ek ∘ i el = e k + l – 1for any i = 1,…, k . In particular,
. Let us denote by ek the unit element in the symmetric group Sk . We obviously have ek ∘ i el = e k + l – 1for any i = 1,…, k . In particular,
[1.73] 
Now let V be an algebra over the operad ASSOC, and let Φ : ASSOC → Endop( V ) be the corresponding morphism of operads. Let μ : V ⊗ V → V be the binary operation Φ ( e2 ). In view of equation [1.73]we have:
[1.74] 
In other words, μ is associative. As ek can be obtained, for any k ≥ 3, by iteratively composing k – 2 times the element e 2, we see that any element of ASSOC kcan be obtained from e 2, partial compositions, symmetric group actions and linear combinations. As a result, any k -ary operation on V , which is in the image of Φ, can be obtained in terms of the associative product μ , partial compositions, symmetric group actions and linear combinations. Summing up, an algebra over the operad ASSOC is nothing but an associative algebra. In view of equation [1.69], the free ASSOC-algebra over a vector space W is the (non-unital) tensor algebra 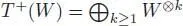 .
.
In the same line of thoughts, the operad governing unital associative algebras is defined similarly, except that the space of 0-ary operations is k.e 0, with ek ∘ i e 0= e k – 1for any i = 1,…, k . The unit element u : k → V of the algebra V is given by u = Φ( e 0). The free unital algebra over a vector space W is the full tensor algebra  .
.
This operad governs commutative associative algebras. COM nis one-dimensional for any n ≥ 1, given by 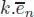 for any n ≥ 0, whereas COM 0:= {0}. The right action of Sn on COM nis trivial. The partial compositions are defined by:
for any n ≥ 0, whereas COM 0:= {0}. The right action of Sn on COM nis trivial. The partial compositions are defined by:
[1.75] 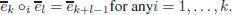
The three axioms of an operad are obviously verified. Let V be an algebra over the operad COM, and let Φ : COM → Endop( V ) be the corresponding morphism of operads. Let μ : V ⊗ V → V be the binary operation  . We obviously have:
. We obviously have:
[1.76] 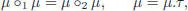
where 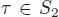 is the flip. Hence, μ is associative and commutative. Here, any k -ary operation in the image of Φ can be obtained, up to a scalar, by iteratively composing
is the flip. Hence, μ is associative and commutative. Here, any k -ary operation in the image of Φ can be obtained, up to a scalar, by iteratively composing 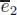 with itself. Hence, an algebra over the operad COM is nothing but a commutative associative algebra. In view of [1.69], the free COM-algebra over a vector space W is the (non-unital) symmetric algebra
with itself. Hence, an algebra over the operad COM is nothing but a commutative associative algebra. In view of [1.69], the free COM-algebra over a vector space W is the (non-unital) symmetric algebra 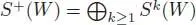 .
.
The operad governing unital commutative associative algebras is defined similarly, except that the space of 0-ary operations is 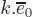 , with
, with 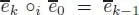 for any i = 1,…, k . The unit element u : k → V of the algebra V is given by u = Φ( e 0). The free unital algebra over a vector space W is the full symmetric algebra
for any i = 1,…, k . The unit element u : k → V of the algebra V is given by u = Φ( e 0). The free unital algebra over a vector space W is the full symmetric algebra 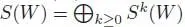 .
.
The map  is easily seen to define a morphism of operads Ψ : ASSOC → COM. Hence, any COM-algebra is also an ASSOC-algebra. This expressed the fact that, forgetting commutativity, a commutative associative algebra is also an associative algebra.
is easily seen to define a morphism of operads Ψ : ASSOC → COM. Hence, any COM-algebra is also an ASSOC-algebra. This expressed the fact that, forgetting commutativity, a commutative associative algebra is also an associative algebra.
1.5.4.3. Associative algebras
Any associative algebra A is some degenerate form of operad: indeed, defining  by
by 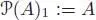 and
and 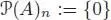 for n ≠ 1, the collection
for n ≠ 1, the collection  is obviously an operad. An algebra over
is obviously an operad. An algebra over  is the same as an A -module.
is the same as an A -module.
This point of view leads to a more conceptual definition of operads: an operad is nothing but an associative unital algebra in the category of “S-objects”, that is, collections of vector spaces 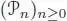 with a right action of Sn on
with a right action of Sn on 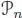 . There is a suitable “tensor product” ⌧ on S-objects, however not symmetric, such that the global composition γ and the unit
. There is a suitable “tensor product” ⌧ on S-objects, however not symmetric, such that the global composition γ and the unit 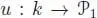 (defined by u (1) = e ) make the following diagrams commute:
(defined by u (1) = e ) make the following diagrams commute:
Читать дальше

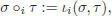
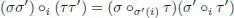
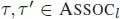 . Let us denote by ek the unit element in the symmetric group Sk . We obviously have ek ∘ i el = e k + l – 1for any i = 1,…, k . In particular,
. Let us denote by ek the unit element in the symmetric group Sk . We obviously have ek ∘ i el = e k + l – 1for any i = 1,…, k . In particular,

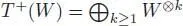 .
. .
.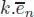 for any n ≥ 0, whereas COM 0:= {0}. The right action of Sn on COM nis trivial. The partial compositions are defined by:
for any n ≥ 0, whereas COM 0:= {0}. The right action of Sn on COM nis trivial. The partial compositions are defined by: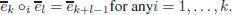
 . We obviously have:
. We obviously have: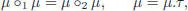
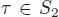 is the flip. Hence, μ is associative and commutative. Here, any k -ary operation in the image of Φ can be obtained, up to a scalar, by iteratively composing
is the flip. Hence, μ is associative and commutative. Here, any k -ary operation in the image of Φ can be obtained, up to a scalar, by iteratively composing 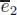 with itself. Hence, an algebra over the operad COM is nothing but a commutative associative algebra. In view of [1.69], the free COM-algebra over a vector space W is the (non-unital) symmetric algebra
with itself. Hence, an algebra over the operad COM is nothing but a commutative associative algebra. In view of [1.69], the free COM-algebra over a vector space W is the (non-unital) symmetric algebra 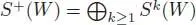 .
.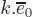 , with
, with 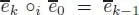 for any i = 1,…, k . The unit element u : k → V of the algebra V is given by u = Φ( e 0). The free unital algebra over a vector space W is the full symmetric algebra
for any i = 1,…, k . The unit element u : k → V of the algebra V is given by u = Φ( e 0). The free unital algebra over a vector space W is the full symmetric algebra 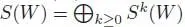 .
. is easily seen to define a morphism of operads Ψ : ASSOC → COM. Hence, any COM-algebra is also an ASSOC-algebra. This expressed the fact that, forgetting commutativity, a commutative associative algebra is also an associative algebra.
is easily seen to define a morphism of operads Ψ : ASSOC → COM. Hence, any COM-algebra is also an ASSOC-algebra. This expressed the fact that, forgetting commutativity, a commutative associative algebra is also an associative algebra. by
by 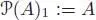 and
and 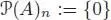 for n ≠ 1, the collection
for n ≠ 1, the collection 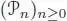 with a right action of Sn on
with a right action of Sn on 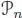 . There is a suitable “tensor product” ⌧ on S-objects, however not symmetric, such that the global composition γ and the unit
. There is a suitable “tensor product” ⌧ on S-objects, however not symmetric, such that the global composition γ and the unit 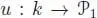 (defined by u (1) = e ) make the following diagrams commute:
(defined by u (1) = e ) make the following diagrams commute:










