Suppose first that k = 1, that is t = B +( t 1) = t 1→ •. Then, we obviously have Fa ( t ) = Fa ( t 1) ⊳ a . Suppose now that Fa ( s ) is unambiguously defined for any tree s with n vertices and k ′ branches with k ′ ≤ k – 1. The equation:
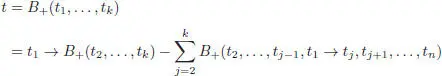
shows that, if Fa ( t ) exists, it is uniquely defined by:
[1.81] 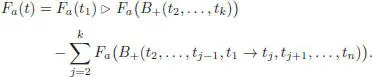
What remains to be shown is that this expression does not depend on the choice of the distinguished branch t 1. In order to see this, choose a second branch (say t 2), and consider the expression:
[1.82] 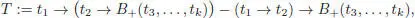
which is obtained by grafting t 1and t 2on B +( t 3, … , tk ). This expression is the sum of five terms:
1 1) T1, obtained by grafting t1 and t2 on the root. It is nothing but the tree t itself.
2 2) T2, obtained by grafting t1 on the root and t2 elsewhere.
3 3) T3, obtained by grafting t2 on the root and t1 elsewhere.
4 4) T4, obtained by grafting t1 on some branch and t2 on some other branch.
5 5) T5, obtained by grafting t1 and t2 on the same branch.
The terms Fa ( T 2) + Fa ( T 3), Fa ( T 4) and Fa ( T 5) are well-defined by the induction hypothesis on the number of branches, and are obviously symmetric in t 1and t 2. We thus arrive at:
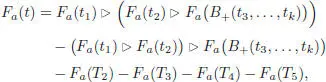
which is symmetric in t 1and t 2thanks to the left pre-Lie relation in A . The expression [1.81]is then the same if we exchange t 1with the branch t 2or any other branch; hence, it is invariant by any permutation of the branches t 1,…, t n. This proves Theorem 1.4 for one generator. The general case is proven similarly, except we have to replace a ∈ A by a collection { a 1,…, ad }.
1.6.3. Right-sided commutative Hopf algebras and the Loday-Ronco theorem
Loday and Ronco (2010) have found a deep link between pre-Lie algebras and commutative Hopf algebras of a certain type: let ℋ be a commutative Hopf algebra. Following this, we say that ℋ is right-sided if it is free as a commutative algebra, that is, ℋ = S ( V ) for some k -vector space V , and if the reduced coproduct verifies:
[1.83] 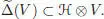
Suppose that V = ⊕ n ≥ 0is graded with finite-dimensional homogeneous components. Then, the graded dual A = V 0is a left pre-Lie algebra, and by the Milnor-Moore theorem, the graded dual ℋ 0is isomorphic to the enveloping algebra 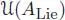 as graded Hopf algebra. Conversely, for any graded pre-Lie algebra A , the graded dual
as graded Hopf algebra. Conversely, for any graded pre-Lie algebra A , the graded dual 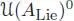 is free commutative right-sided (Loday and Ronco 2010, Theorem 5.3).
is free commutative right-sided (Loday and Ronco 2010, Theorem 5.3).
The Hopf algebra ℋ CKof rooted forests enters into this framework, and, as it was first explicited in Chapoton (2001), the associated pre-Lie algebra is the free pre-Lie algebra of rooted trees with grafting: to see this, denote by ( δs ) the dual basis in the graded dual 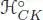 of the forest basis of ℋ CK. The correspondence δ : s ↦ δs extends linearly to a unique vector space isomorphism from ℋ CKonto
of the forest basis of ℋ CK. The correspondence δ : s ↦ δs extends linearly to a unique vector space isomorphism from ℋ CKonto 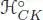 . For any tree t , the corresponding δt is an infinitesimal character of ℋ CK, that is, it is a primitive element of ℋ°. We denote by * the (convolution) product of ℋ°. We have:
. For any tree t , the corresponding δt is an infinitesimal character of ℋ CK, that is, it is a primitive element of ℋ°. We denote by * the (convolution) product of ℋ°. We have:
[1.84] 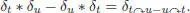
Here, t ↷ u is obtained by grafting t on u , namely:
[1.85] 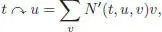
where N ′( t , u , v ) is the number of partitions V ( t ) = V ∐ W, W < V , such that υ | V= t and υ | W= u . Another normalization is often employed: considering the normalized dual basis 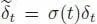 , where σ ( t ) = |Aut t | stands for the symmetry factor of t , we obviously have:
, where σ ( t ) = |Aut t | stands for the symmetry factor of t , we obviously have:
[1.86] 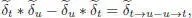
where:
[1.87] 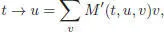
where 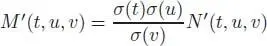 can be interpreted as the number of ways to graft the tree t on the tree u in order to get the tree v . The operation → then coincides with the grafting free pre-Lie operation introduced in section 1.6.1.2 2 .
can be interpreted as the number of ways to graft the tree t on the tree u in order to get the tree v . The operation → then coincides with the grafting free pre-Lie operation introduced in section 1.6.1.2 2 .
The other pre-Lie operation ⊲ of section 1.6.1.2, more precisely its opposite ⊳, is associated with another right-sided Hopf algebra of forests ℋ which has been investigated in Calaque et al . (2011) and Manchon and Saidi (2011), and which can be defined by considering trees as Feynman diagrams (without loops): let 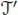 be the vector space spanned by rooted trees with at least one edge. Consider the symmetric algebra
be the vector space spanned by rooted trees with at least one edge. Consider the symmetric algebra  , which can be seen as the k -vector space generated by rooted forests with all connected components containing at least one edge. We identify the unit of
, which can be seen as the k -vector space generated by rooted forests with all connected components containing at least one edge. We identify the unit of 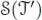 with the rooted tree •. A subforest of a tree t is either the trivial forest •, or a collection ( t 1,…, tn ) of pairwise disjoint subtrees of t , each of them containing at least one edge. In particular, two subtrees of a subforest cannot have any common vertex.
with the rooted tree •. A subforest of a tree t is either the trivial forest •, or a collection ( t 1,…, tn ) of pairwise disjoint subtrees of t , each of them containing at least one edge. In particular, two subtrees of a subforest cannot have any common vertex.
Читать дальше

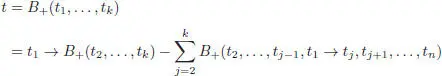
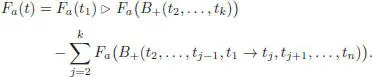
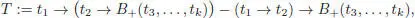
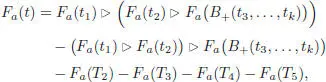
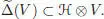
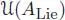 as graded Hopf algebra. Conversely, for any graded pre-Lie algebra A , the graded dual
as graded Hopf algebra. Conversely, for any graded pre-Lie algebra A , the graded dual 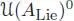 is free commutative right-sided (Loday and Ronco 2010, Theorem 5.3).
is free commutative right-sided (Loday and Ronco 2010, Theorem 5.3).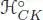 of the forest basis of ℋ CK. The correspondence δ : s ↦ δs extends linearly to a unique vector space isomorphism from ℋ CKonto
of the forest basis of ℋ CK. The correspondence δ : s ↦ δs extends linearly to a unique vector space isomorphism from ℋ CKonto 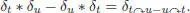
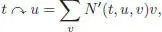
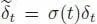 , where σ ( t ) = |Aut t | stands for the symmetry factor of t , we obviously have:
, where σ ( t ) = |Aut t | stands for the symmetry factor of t , we obviously have: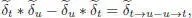
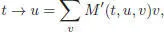
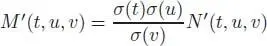 can be interpreted as the number of ways to graft the tree t on the tree u in order to get the tree v . The operation → then coincides with the grafting free pre-Lie operation introduced in section 1.6.1.2 2 .
can be interpreted as the number of ways to graft the tree t on the tree u in order to get the tree v . The operation → then coincides with the grafting free pre-Lie operation introduced in section 1.6.1.2 2 .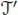 be the vector space spanned by rooted trees with at least one edge. Consider the symmetric algebra
be the vector space spanned by rooted trees with at least one edge. Consider the symmetric algebra  , which can be seen as the k -vector space generated by rooted forests with all connected components containing at least one edge. We identify the unit of
, which can be seen as the k -vector space generated by rooted forests with all connected components containing at least one edge. We identify the unit of 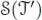 with the rooted tree •. A subforest of a tree t is either the trivial forest •, or a collection ( t 1,…, tn ) of pairwise disjoint subtrees of t , each of them containing at least one edge. In particular, two subtrees of a subforest cannot have any common vertex.
with the rooted tree •. A subforest of a tree t is either the trivial forest •, or a collection ( t 1,…, tn ) of pairwise disjoint subtrees of t , each of them containing at least one edge. In particular, two subtrees of a subforest cannot have any common vertex.










