where α is the multiplicatively extended to forests, β is seen as an infinitesimal character of ℋ CK, and * is the dualization of the left coaction Φ of ℋ on ℋ CK defined in section 1.6.3 .
The condition α (•) = 1 is in fact dropped in Calaque et al . (2011, Proposition 15): the price to pay is that one has to replace the Hopf algebra ℋ by a non-connected bialgebra 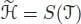 with a suitable coproduct, such that ℋ is obtained as the quotient
with a suitable coproduct, such that ℋ is obtained as the quotient 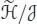 , where
, where 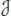 is the ideal generated by • – 1. The substitution product * then coincides with the one considered in Chartier et al . (2010) via natural identifications.
is the ideal generated by • – 1. The substitution product * then coincides with the one considered in Chartier et al . (2010) via natural identifications.
1.7. Other related algebraic structures
1.7.1. NAP algebras
NAP algebras (NAP for Non-Associative Permutative) appear under this name in Livernet (2006), and under the name “left- (right-)commutative algebras” in Dzhumadil’daev and Löfwall (2002). They can be seen in some sense as a “simplified version” of pre-Lie algebras. Saidi showed that the pre-Lie operad is a deformation of the NAP operad in a precise sense, involving the notion of current-preserving operad (Saidi 2014).
1.7.1.1. Definition and general properties
A left NAP algebra over a field k is a k -vector space A with a bilinear binary composition ▶ that satisfies the left NAP identity:
[1.105] 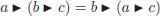
for any a, b, c ∈ A . Analogously, a right NAP algebra is a k -vector space A with a binary composition ◀ satisfying the right NAP identity:
[1.106] 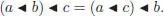
As any right NAP algebra is also a left NAP algebra with product a ▶ b := b ◀ a , we can stick to left NAP algebras, which is what we will do unless specifically indicated.
1.7.1.2. Free NAP algebras
The left Butcher product s ∘ t of two rooted trees s and t is defined by grafting s on the root of t . For example:
[1.107] 
The following theorem is due to Dzhumadil’daev and Löfwall (2002) (see Livernet (2006) for an operadic approach):
THEOREM 1.5.– The free NAP algebra with d generators is the vector space spanned by rooted trees with d colors, endowed with the left Butcher product .
PROOF.– We give the proof for one generator, the case of d generators being entirely similar. The left NAP property for the Butcher product is obvious. Let ( A , ▶) be any left NAP algebra, and let a ∈ A . We have to prove that there exists a unique left NAP algebra morphism Ga from 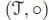 to ( A , ▶), such that Ga (•) = a . As in the pre-Lie case, we proceed by double induction, first on the number n of vertices, and second on the number k of branches. In the case k = 1, the tree t writes B +( t 1) = t 1∘ ∙; hence, Ga ( t ) = Ga ( s ) ▶ a is the only possible choice. Now a tree with k branches writes:
to ( A , ▶), such that Ga (•) = a . As in the pre-Lie case, we proceed by double induction, first on the number n of vertices, and second on the number k of branches. In the case k = 1, the tree t writes B +( t 1) = t 1∘ ∙; hence, Ga ( t ) = Ga ( s ) ▶ a is the only possible choice. Now a tree with k branches writes:
[1.108] 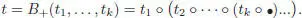
The only possible choice is then:
[1.109] 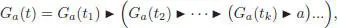
and the result is clearly symmetric in t 1and t 2due to the left NAP identity in A . Using the induction hypothesis, the result is also invariant under permutation of the branches 2,3,…, k . Hence, it is invariant under the permutation of all branches, which proves the theorem. □
Despite the similarity with the pre-Lie situation described in section 1.6.2, the NAP framework is much simpler due to the set-theoretic nature of the Butcher product: for any trees s and t , the Butcher product s ∘ t is a tree, whereas the grafting s → t is a sum of trees. We obtain for the first trees:
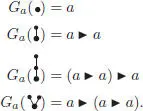
1.7.1.3. NAP algebras of vector fields
We consider the flat affine n -dimensional space En although it is possible, through parallel transport, to consider any smooth manifold endowed with a flat torsion-free connection. Fix an origin in En , which will be denoted by O . For vector fields 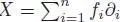 and
and 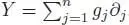 , we set:
, we set:
[1.110] 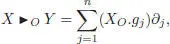
where 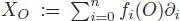 is the constant vector field obtained by freezing the coefficients of X at x = O .
is the constant vector field obtained by freezing the coefficients of X at x = O .
PROPOSITION 1.17.– The space χ (ℝ n) of vector fields endowed with product ▶ O is a left NAP algebra. Moreover, for any other choice of origin O’ ∈ En, the conjugation with the translation of vector 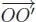 is an isomorphism from ( χ (ℝ n), ▶ O )) onto ( χ (ℝ n), ▶ O’)).
is an isomorphism from ( χ (ℝ n), ▶ O )) onto ( χ (ℝ n), ▶ O’)).
PROOF.– Let 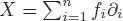 ,
, 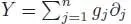 and
and 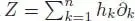 be three vector fields. Then:
be three vector fields. Then:
Читать дальше

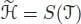 with a suitable coproduct, such that ℋ is obtained as the quotient
with a suitable coproduct, such that ℋ is obtained as the quotient 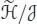 , where
, where 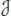 is the ideal generated by • – 1. The substitution product * then coincides with the one considered in Chartier et al . (2010) via natural identifications.
is the ideal generated by • – 1. The substitution product * then coincides with the one considered in Chartier et al . (2010) via natural identifications.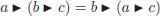
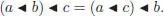

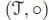 to ( A , ▶), such that Ga (•) = a . As in the pre-Lie case, we proceed by double induction, first on the number n of vertices, and second on the number k of branches. In the case k = 1, the tree t writes B +( t 1) = t 1∘ ∙; hence, Ga ( t ) = Ga ( s ) ▶ a is the only possible choice. Now a tree with k branches writes:
to ( A , ▶), such that Ga (•) = a . As in the pre-Lie case, we proceed by double induction, first on the number n of vertices, and second on the number k of branches. In the case k = 1, the tree t writes B +( t 1) = t 1∘ ∙; hence, Ga ( t ) = Ga ( s ) ▶ a is the only possible choice. Now a tree with k branches writes: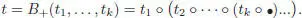
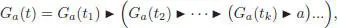
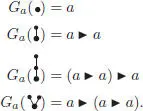
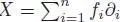 and
and 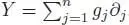 , we set:
, we set: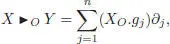
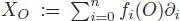 is the constant vector field obtained by freezing the coefficients of X at x = O .
is the constant vector field obtained by freezing the coefficients of X at x = O .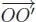 is an isomorphism from ( χ (ℝ n), ▶ O )) onto ( χ (ℝ n), ▶ O’)).
is an isomorphism from ( χ (ℝ n), ▶ O )) onto ( χ (ℝ n), ▶ O’)).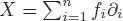 ,
, 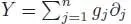 and
and 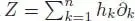 be three vector fields. Then:
be three vector fields. Then:










