Algebra and Applications 2

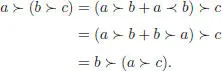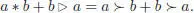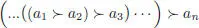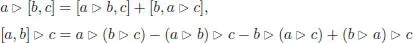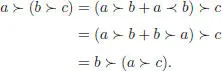
There also exists a twisted version of dendriform algebras, encompassing operators like the Jackson integral Iq (Ebrahimi-Fard and Manchon 2011). Returning to ordinary dendriform algebras, we observe that:

[1.124]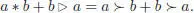

This identity generalizes to any number of elements, expressing the symmetrization of

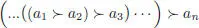
in terms of the associative product and the left pre-Lie product (Ebrahimi-Fard et al . 2008). For more on dendriform algebras and the associated pre-Lie structures, see Ebrahimi-Fard et al . (2008), Ebrahimi-Fard and Manchon (2009a, 2009b, 2011) and Ebrahimi-Fard’s note in the present volume.

Post-Lie algebras have been introduced by Vallette (2007), independent of the introduction of the closely related notion of D-algebra in Munthe-Kaas and Wright (2008). A left post-Lie algebra on a field k is a k -vector space A together with a bilinear binary product ⊳ and a Lie bracket [–, –], such that

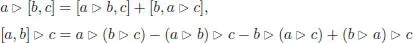
for any a , b , c ∈ A . In particular, a post-Lie algebra A is a pre-Lie algebra if and only if the Lie bracket vanishes. The space of vector fields on a Lie group is a post-Lie algebra, and the free post-Lie algebra with one generator is the free Lie algebra on the linear span of planar rooted trees. The binary product ⊳ is given by left grafting , which is not pre-Lie anymore because of planarity. This is the starting point to the Lie-Butcher theory (see, for example, Lundervold and Munthe-Kaas (2013); Ebrahimi-Fard et al . (2015); Curry et al . (2019, 2020)).

Agrachev, A. and Gamkrelidze, R. (1981). Chronological algebras and nonstationary vector fields. J. Sov. Math ., 17(1), 1650–1675.

Andruskiewitsch, N. and Cuadra, J. (2013). On the structure of (co-Frobenius) Hopf algebras. J. Noncommutative Geom ., 13(1), 83–104.

Andruskiewitsch, N. and Schneider, H.-J. (2002). Pointed Hopf algebras. In New Directions in Hopf Algebras , Montgomery, S. and Schneider, H.-J. (eds). MSRI and Cambridge University Press, Cambridge.

Balinskii, A.A. and Novikov, S.P. (1985). Poisson bracket of hydrodynamic type, Frobenius algebras and Lie algebras. Doklady An. SSSR , 283(5), 1036–1039.

Brouder, C. (2000). Runge-Kutta methods and renormalization. Eur. Phys. J ., C12, 512-534.

Burde, D. (2006). Left-symmetric algebras or pre-Lie algebras in Geometry and Physics. Central Eur. J. Math . DOI: 10.2478/s11533–006–0014–9.

Butcher, J.C. (1963). Coefficients for the study of Runge-Kutta integration processes. J. Austral. Math. Soc , 3, 185-201.

Calaque, D., Ebrahimi-Fard, K., Manchon, D. (2011). Two interacting Hopf algebras of trees: A Hopf-algebraic approach to composition and substitution of B-series. Adv. Appl. Math ., 47(2), 282-308.

Cayley, A. (1857). On the theory of analytical forms called trees. Phil. Mag ., 13, 172-176.

Chapoton, F. (2001). Algèbres pré-Lie et algèbres de Hopf liées à la renormalisation. C. R. Acad. Sci ., 332(1), 681–684.

Chapoton, F. (2002). Rooted trees and an exponential-like series. arXiv:math/0209104.

Chapoton, F. and Livernet, M. (2001). Pre-Lie algebras and the rooted trees operad. Int. Math. Res. Not ., 2001, 395–408.

Chartier, P., Hairer, E., Vilmart, G. (2005). A substitution law for B -series vector fields. Research report, INRIA, Rocquencourt.

Chartier, P., Hairer, E., Vilmart, G. (2010). Algebraic structures of B -series. Found. Comput. Math ., 10, 407–427.

Connes, A. and Kreimer, D. (1998). Hopf algebras, renormalization and noncommutative geometry. Comm. Math. Phys ., 199, 203–242.

Curry, C., Ebrahimi-Fard, K., Munthe-Kaas, H.Z. (2019). What is a post-Lie algebra and why is it useful in geometric integration. In Numerical Mathematics and Advanced Applications ENUMATH 2017 , Radu, F., Kumar, K., Berre, I., Nordbotten, J.M., Pop, I.S. (eds). Springer, Cham [Online]. Available at: https://doi.org/10.1007/978–3–319–96415–738.

Curry, C., Ebrahimi-Fard, K., Manchon, D., Munthe-Kaas, H.Z. (2020). Planary branched rough paths and rough differential equations on homogeneous spaces. J. Diff. Eq ., 269(11), 9740–9782.

Dǎscǎlescu, S., Nǎstǎsescu, C., Raianu, S. (2001). Hopf Algebras: An Introduction . Marcel Dekker, New York.

Dür, A. (1986). Möbius Functions, Incidence Algebras and Power Series Representations . Springer, Berlin, Heidelberg.

Dzhumadil’daev, A. and Löfwall, C. (2002). Trees, free right-symmetric algebras, free Novikov algebras and identities. Homol. Homotopy Appl ., 4(2), 165–190.

Ebrahimi-Fard, K. and Manchon, D. (2009a). Dendriform equations. J. Algebra , 322, 4053–4079.

Ebrahimi-Fard, K. and Manchon, D. (2009b). A Magnus- and Fer-type formula in dendriform algebras. Found. Comput. Math ., 9(3), 295–316.

Ebrahimi-Fard, K. and Manchon, D. (2011). Twisted dendriform algebras and the pre-Lie Magnus expansion. J. Pure Appl. Alg ., 215(11), 2615–2627.

Ebrahimi-Fard, K., Manchon, D., Patras, F. (2008). New identities in dendriform algebras. J. Algebra , 320, 708–727.

Ebrahimi-Fard, K., Lundervold, A., Munthe-Kaas, H.Z. (2015). On the Lie enveloping algebra of a Post-Lie algebra. J. Lie Theory , 25(4), 1139–1165.

Gerstenhaber, M. (1963). The cohomology structure of an associative ring. Ann. Math ., 78, 267–288.

Guin, D. and Oudom, J.-M. (2005). Sur l’algèbre enveloppante d’une algèbre pré-Lie. C. R. Acad. Sci ., 340(1).

Hairer, E., Lubich, C., Wanner, G. (2002). Geometric Numerical Tntegration, Structure-Preserving Algorithms for Ordinary Differential Equations . Springer, Berlin.

Hentzel, I.R., Jacobs, D.P., Peresi, A. (1996). A basis for free assosymmetric algebras. J. Algebra , 183(2), 306–318.

Kassel, C. (1995). Quantum Groups . Springer-Verlag, New York.

Kleinfeld, E. (1957). Assosymmetric rings. Proc. Amer. Math. Soc ., 8(5), 983–986.

Kreimer, D. (2002). The combinatorics of (perturbative) quantum field theories. Phys. Rep ., 363, 387–424.

Livernet, M. (2006). A rigidity theorem for pre-Lie algebras. J. Pure Appl. Alg ., 207(1), 1–18.

Loday, J.-L. (1995). Cup-product for Leibniz cohomology and dual Leibniz algebras. Math. Scand ., 77(2), 189–196.

Loday, J.-L. (1996). La renaissance des opérades. In Séminaire Bourbaki : Volume 1994/95, Exposés 790–804 , Société mathématique de France (ed.). Astérisque, France.

Loday, J.-L. (2001). Dialgebras. In Dialgebras and Related Operads , Loday, J.-L., Frabetti, A., Chapoton, F., Goichot, F. (eds). Springer, Berlin.

Loday, J.-L. and Ronco, M. (2010). Combinatorial Hopf algebras. Clay Math. Proc ., 11.