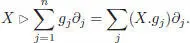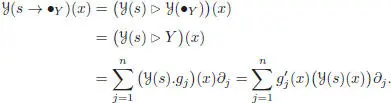Let s be a subforest of a rooted tree t . Denote by t / s the tree obtained by contracting each connected component of s onto a vertex. We turn ℋ into a bialgebra by defining a coproduct Δ : ℋ → ℋ ⊗ ℋ on each tree 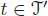 by :
by :
[1.88] 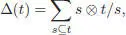
where the sum runs over all possible subforests (including the unit • and the full subforest t ). As usual we extend the coproduct Δ multiplicatively onto 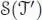 . In fact, coassociativity is easily verified. This makes ℋ := ⊕ n ≥ 0ℋ na connected graded bialgebra, hence a Hopf algebra, where the grading is defined in terms of the number of edges. The antipode S : ℋ → ℋ is given (recursively with respect to the number of edges) by one of the two following formulae:
. In fact, coassociativity is easily verified. This makes ℋ := ⊕ n ≥ 0ℋ na connected graded bialgebra, hence a Hopf algebra, where the grading is defined in terms of the number of edges. The antipode S : ℋ → ℋ is given (recursively with respect to the number of edges) by one of the two following formulae:
[1.89] 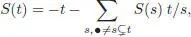
[1.90] 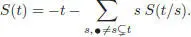
It turns out that ℋ CKis left comodule-bialgebra over ℋ (Calaque et al . 2011; Manchon and Saidi 2011), in the sense that the following diagram commutes:
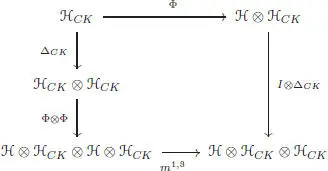
Here, the coaction Φ : ℋ CK→ ℋ ⊗ ℋ CKis the algebra morphism given by Φ( 1) = • ⊗ 1and Φ( t ) = Δ ℋ( t ) for any nonempty tree t . As a result, the group of characters of ℋ acts on the group of characters of ℋ CKby automorphisms.
1.6.4. Pre-Lie algebras of vector fields
1.6.4.1. Flat torsion-free connections
Let M be a differentiable manifold, and let ▽ be the covariant derivation operator associated with a connection on the tangent bundle TM . The covariant derivation is a bilinear operator on vector fields (i.e. two sections of the tangent bundle): ( X, Y ) ↦ ▽ XY , such that the following axioms are fulfilled:
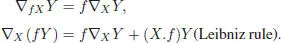
The torsion of the connection  is defined by:
is defined by:
[1.91] 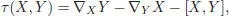
and the curvature tensor is defined by:
[1.92] 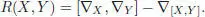
The connection is flat if the curvature R vanishes identically, and torsion-free if 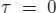 . The following crucial observation by Matsushima (1968, Lemma 1) is an immediate consequence of equation [1.43]:
. The following crucial observation by Matsushima (1968, Lemma 1) is an immediate consequence of equation [1.43]:
PROPOSITION 1.14.– For any smooth manifold M endowed with aflat torsion-free connection ▽, the space χ ( M ) of vector fields is a left pre-Lie algebra, with pre-Lie product given by :
[1.93] 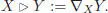
Note that on M = ℝ n, endowed with its canonical flat torsion-free connection, the pre-Lie product is given by:
[1.94] 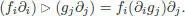
1.6.4.2. Relating two pre-Lie structures
Cayley (1857) discovered a link between rooted trees and vector fields on the manifold ℝ n, endowed with its natural flat torsion free connection, which can be described in modern terms as follows: let  be the free pre-Lie algebra on the space of vector fields on ℝ n. A basis of
be the free pre-Lie algebra on the space of vector fields on ℝ n. A basis of  is given by rooted trees with vertices decorated by some basis of χ (ℝ n). There is a unique pre-Lie algebra morphism
is given by rooted trees with vertices decorated by some basis of χ (ℝ n). There is a unique pre-Lie algebra morphism 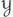 , the Cayley map , such that
, the Cayley map , such that 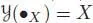 for any vector field X .
for any vector field X .
PROPOSITION 1.15.– For any rooted tree t, with each vertex v being decorated by a vector field Xv, the vector field 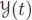 is given at x ∈ ℝ n by the following recursive procedure (Hairer et al. 2002): if the decorated tree t is obtained by grafting all of its branches tk on the root r decorated by the vector field , that is, ifit writes , then :
is given at x ∈ ℝ n by the following recursive procedure (Hairer et al. 2002): if the decorated tree t is obtained by grafting all of its branches tk on the root r decorated by the vector field , that is, ifit writes , then :
[1.95] 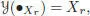
[1.96] 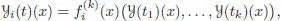
where stands for the k th differential of fi .
PROOF. – From equation [1.94], for any vector field X and any other vector field 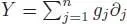 :
:
[1.97] 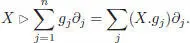
In other words, X ⊳ Y is the derivative of Y along the vector field X , where Y is viewed as a C ∞map from ℝ nto ℝ n. We prove the result by induction on the number k of branches: for k = 1, we check:
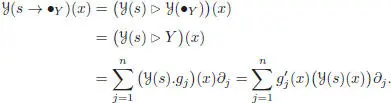
Now, we can compute, using the Leibniz rule and the induction hypothesis (we drop the point x ∈ ℝ nwhere the vector fields are evaluated):
Читать дальше

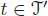 by :
by :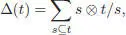
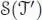 . In fact, coassociativity is easily verified. This makes ℋ := ⊕ n ≥ 0ℋ na connected graded bialgebra, hence a Hopf algebra, where the grading is defined in terms of the number of edges. The antipode S : ℋ → ℋ is given (recursively with respect to the number of edges) by one of the two following formulae:
. In fact, coassociativity is easily verified. This makes ℋ := ⊕ n ≥ 0ℋ na connected graded bialgebra, hence a Hopf algebra, where the grading is defined in terms of the number of edges. The antipode S : ℋ → ℋ is given (recursively with respect to the number of edges) by one of the two following formulae: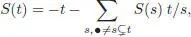
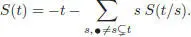

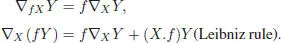
 is defined by:
is defined by: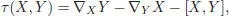
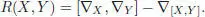
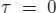 . The following crucial observation by Matsushima (1968, Lemma 1) is an immediate consequence of equation [1.43]:
. The following crucial observation by Matsushima (1968, Lemma 1) is an immediate consequence of equation [1.43]: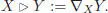
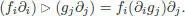
 be the free pre-Lie algebra on the space of vector fields on ℝ n. A basis of
be the free pre-Lie algebra on the space of vector fields on ℝ n. A basis of 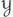 , the Cayley map , such that
, the Cayley map , such that 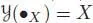 for any vector field X .
for any vector field X .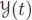 is given at x ∈ ℝ n by the following recursive procedure (Hairer et al. 2002): if the decorated tree t is obtained by grafting all of its branches tk on the root r decorated by the vector field , that is, ifit writes , then :
is given at x ∈ ℝ n by the following recursive procedure (Hairer et al. 2002): if the decorated tree t is obtained by grafting all of its branches tk on the root r decorated by the vector field , that is, ifit writes , then :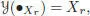
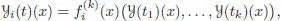
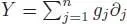 :
: