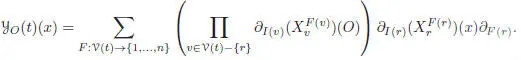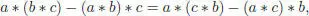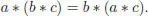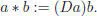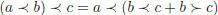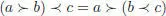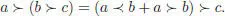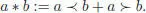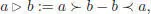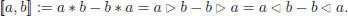[1.111] 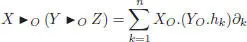
is symmetric in X and Y , due to the fact that the two constant vector fields XO and YO commute. The second assertion is left as an exercise for the reader. □
With the notations of section 1.6.4, there is a unique NAP algebra morphism
[1.112] 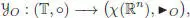
the frozen Cayley map , such that 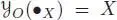 . By also considering the unique NAP algebra morphism
. By also considering the unique NAP algebra morphism 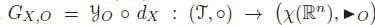 , the maps GX,O ( t ) : ℝ n→ ℝ nare called the frozen elementary differentials .
, the maps GX,O ( t ) : ℝ n→ ℝ nare called the frozen elementary differentials .
PROPOSITION 1.18.– For any rooted tree t, each vertex v being decorated by a vector field Xv, the vector field is given at x ∈ ℝ n by the following recursive procedure: if the decorated tree t is obtained by grafing all of its branches tk on the root r decorated by the vector field , that is, if it writes , then :
[1.113] 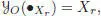
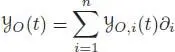 with:
with:
[1.114] 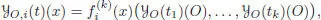
where 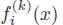 stands for the k th differential of fi, evaluated at x .
stands for the k th differential of fi, evaluated at x .
PROOF.– We prove the result by induction on the number k of branches: for k = 1, we check:

Now we can compute using the induction hypothesis and the fact that the vector fields 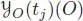 are constant:
are constant:
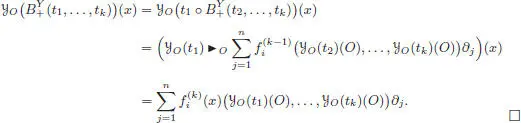
COROLLARY 1.3 (closed formula).– With the notations of Corollary 1.2, for any rooted tree t with set of vertices 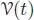 and root r, each vertex v being decorated by a vector field
and root r, each vertex v being decorated by a vector field 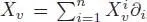 , the vector field
, the vector field 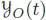 is given at x ∈ ℝ n by the following formula:
is given at x ∈ ℝ n by the following formula:
[1.115] 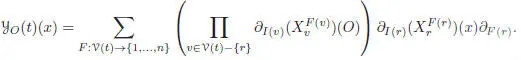
A Novikov algebra is a right pre-Lie algebra which is also left NAP, namely, a vector space A together with a bilinear product ∗, such that, for any a , b , c ∈ A , we have:
[1.116] 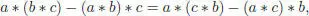
[1.117] 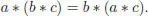
Novikov algebras first appeared in hydrodynamical equations (Balinskii and Novikov 1985; Osborn 1992). The prototype is a commutative associative algebra together with a derivation D , with the Novikov product being given by:
[1.118] 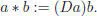
The free Novikov algebra on a set of generators has been given in Dzhumadil’daev and Löfwall (2002, section 7) in terms of some classes of rooted trees.
1.7.3. Assosymmetric algebras
An assosymmetric algebra is a vector space endowed with a bilinear operation that is both left and right pre-Lie, which means that the associator a * ( b * c ) – ( a ∗ b ) ∗ c is symmetric under the permutation group S 3. This notion was introduced by Kleinfeld (1957) (see also Hentzel et al . (1996)). All associative algebras are obviously assosymmetric; however, the converse is not true.
1.7.4. Dendriform algebras
A dendriform algebra (Loday 2001) over the field k is a k -vector space A endowed with two bilinear operations, denoted ≺ and ≻ and called right and left products, respectively, subject to the three axioms below:
[1.119] 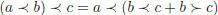
[1.120] 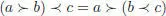
[1.121] 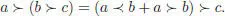
We readily verify that these relations yield associativity for the product
[1.122] 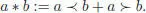
However, at the same time-ordering, the dendriform relations imply that the bilinear product ⊳ defined by:
[1.123] 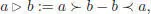
is left pre-Lie. The associative operation * and the pre-Lie operation ⊳ define the same Lie bracket, and this is, of course, still true for the opposite (right) pre-Lie product ⊲:
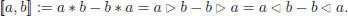
In the commutative case (commutative dendriform algebras are also named Zinbiel algebras (Loday 1995, 2001), the left and right operations are further required to identify, so that a ≻ b = b ≺ a . In this case, both pre-Lie products vanish. A natural example of a commutative dendriform algebra is given by the shuffle algebra in terms of half-shuffles (Schützenberger 1958/1959). Any associative algebra A equipped with a linear integral-like map I : A → A satisfying the integration by parts rule also gives a dendriform algebra, when a ≺ b := aI ( b ) and a ≻ b := I ( a ) b . The left pre-Lie product is then given by a ⊳ b = [ I ( a ), b ]. It is worth mentioning that Zinbiel algebras are also NAP algebras, as shown by the computation below (dating back to Schützenberger (1958/1959)):
Читать дальше

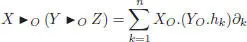
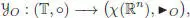
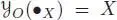 . By also considering the unique NAP algebra morphism
. By also considering the unique NAP algebra morphism 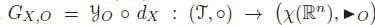 , the maps GX,O ( t ) : ℝ n→ ℝ nare called the frozen elementary differentials .
, the maps GX,O ( t ) : ℝ n→ ℝ nare called the frozen elementary differentials .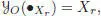
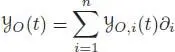 with:
with: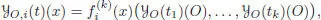
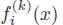 stands for the k th differential of fi, evaluated at x .
stands for the k th differential of fi, evaluated at x .
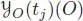 are constant:
are constant: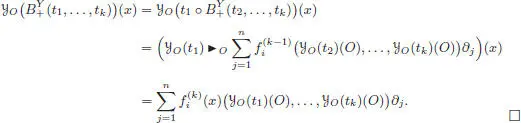
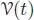 and root r, each vertex v being decorated by a vector field
and root r, each vertex v being decorated by a vector field 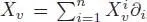 , the vector field
, the vector field 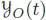 is given at x ∈ ℝ n by the following formula:
is given at x ∈ ℝ n by the following formula: