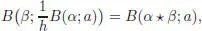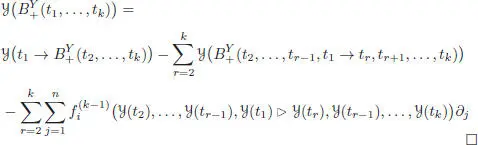
COROLLARY 1.2 (closed formula).– For any rooted tree t with set of vertices and root r, each vertex v being decorated by a vector field , the vector field is given at x ∈ ℝn by the following formula:
[1.98] 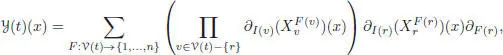
with the shorthand notation:
[1.99] 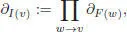
where the product runs over the incoming vertices of v .
Now fix a vector field X on ℝ nand consider the map dX from undecorated rooted trees to vector field-decorated rooted trees, which decorates each vertex by X . It is obviously a pre-Lie algebra morphism, and 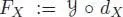 is the unique pre-Lie algebra morphism that sends the one-vertex tree • to the vector field X .
is the unique pre-Lie algebra morphism that sends the one-vertex tree • to the vector field X .
1.6.5. B-series, composition and substitution
B-series have been defined by Hairer and Wanner, following the pioneering work of Butcher (1963) on Runge-Kutta methods for the numerical resolution of differential equations. Remarkably enough, rooted trees revealed to be an adequate tool not only for vector fields, but also for the numerical approximation of their integral curves. Butcher discovered that the Runge-Kutta methods formed a group (since then called the Butcher group), which was nothing but the character group of the Connes-Kreimer Hopf algebra ℋ CK(Brouder 2000).
Consider any left pre-Lie algebra ( A , ⊳), and introduce a fictitious unit 1, such that 1⊳ a = a ⊳ 1= a for any a ∈ A , and consider for any a ∈ A , the unique left pre-Lie algebra morphism Fa : (T, →) → ( A , ⊳), such that Fa (•) = a . A B-series is an element of hA [[ h ]] ⊕ k . 1defined by:
[1.100] 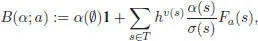
where α is any linear form on  (here, σ ( s ) is the symmetry factor of the tree, that is, the order of its group of automorphisms). It matches the usual notion of B -series (Hairer et al . 2002) when A is the pre-Lie algebra of vector fields on ℝ n(it is also convenient to set Fa (∅) = 1). In this case, the vector fields Fa ( t ) for a tree t are differentiable maps from ℝ nto ℝ ncalled elementary differentials. B -series can be composed coefficient wise, as series in the indeterminate h , whose coefficients are maps from ℝ nto ℝ n. The same definition with trees decorated by a set of colors
(here, σ ( s ) is the symmetry factor of the tree, that is, the order of its group of automorphisms). It matches the usual notion of B -series (Hairer et al . 2002) when A is the pre-Lie algebra of vector fields on ℝ n(it is also convenient to set Fa (∅) = 1). In this case, the vector fields Fa ( t ) for a tree t are differentiable maps from ℝ nto ℝ ncalled elementary differentials. B -series can be composed coefficient wise, as series in the indeterminate h , whose coefficients are maps from ℝ nto ℝ n. The same definition with trees decorated by a set of colors 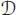 leads to straightforward generalizations. For example, the P -series used in partitioned Runge-Kutta methods (Hairer et al . 2002) correspond to bi-coloured trees.
leads to straightforward generalizations. For example, the P -series used in partitioned Runge-Kutta methods (Hairer et al . 2002) correspond to bi-coloured trees.
A slightly different way of defining B -series is the following: consider the unique pre-Lie algebra morphism 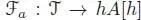 , such that ℱ a (•) = ha . It respects the gradings given by the number of vertices and the powers of h , respectively; hence, it extends to
, such that ℱ a (•) = ha . It respects the gradings given by the number of vertices and the powers of h , respectively; hence, it extends to  , where
, where  is the completion of
is the completion of 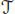 with respect to the grading. We further extend it to the empty tree by setting ∙ a(∅) = 1. We then have:
with respect to the grading. We further extend it to the empty tree by setting ∙ a(∅) = 1. We then have:
[1.101] 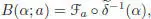
where 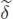 is the isomorphism from
is the isomorphism from 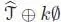 to
to  given by the normalized dual basis (see section 1.6.3).
given by the normalized dual basis (see section 1.6.3).
We restrict ourselves to B -series B ( α ; a ) with α (∅) = 1. Such α s are in one-to-one correspondence with characters of the algebra of forests (which is the underlying algebra of ℋ CK) by setting:
[1.102] 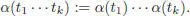
The Hairer-Wanner theorem (Hairer et al . 2002, Theorem III.1.10) says that the composition of B -series corresponds to the convolution product of characters of ℋ CK, namely:
[1.103] 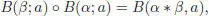
where linear forms α, β on  and their character counterparts are identified modulo the above correspondence.
and their character counterparts are identified modulo the above correspondence.
Let us now turn to substitution (Chartier et al . 2010). The idea is to replace the vector field a in a B -series B ( β ; a ) by another vector field  , which expresses itself as a B -series, that is,
, which expresses itself as a B -series, that is, 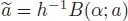 , where α is now a linear form on
, where α is now a linear form on 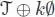 , such that α (∅) = 0. Here, we suppose that α (•) = 1. The following proposition is proven in Calaque et al . (2011):
, such that α (∅) = 0. Here, we suppose that α (•) = 1. The following proposition is proven in Calaque et al . (2011):
PROPOSITION 1.16.– For any linear forms α,β on with α (• = 1), we have :
[1.104] 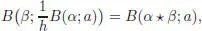
Читать дальше

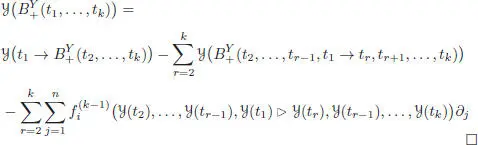
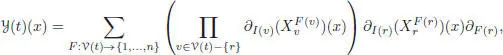
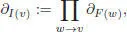
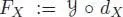 is the unique pre-Lie algebra morphism that sends the one-vertex tree • to the vector field X .
is the unique pre-Lie algebra morphism that sends the one-vertex tree • to the vector field X .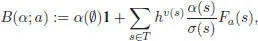
 (here, σ ( s ) is the symmetry factor of the tree, that is, the order of its group of automorphisms). It matches the usual notion of B -series (Hairer et al . 2002) when A is the pre-Lie algebra of vector fields on ℝ n(it is also convenient to set Fa (∅) = 1). In this case, the vector fields Fa ( t ) for a tree t are differentiable maps from ℝ nto ℝ ncalled elementary differentials. B -series can be composed coefficient wise, as series in the indeterminate h , whose coefficients are maps from ℝ nto ℝ n. The same definition with trees decorated by a set of colors
(here, σ ( s ) is the symmetry factor of the tree, that is, the order of its group of automorphisms). It matches the usual notion of B -series (Hairer et al . 2002) when A is the pre-Lie algebra of vector fields on ℝ n(it is also convenient to set Fa (∅) = 1). In this case, the vector fields Fa ( t ) for a tree t are differentiable maps from ℝ nto ℝ ncalled elementary differentials. B -series can be composed coefficient wise, as series in the indeterminate h , whose coefficients are maps from ℝ nto ℝ n. The same definition with trees decorated by a set of colors  leads to straightforward generalizations. For example, the P -series used in partitioned Runge-Kutta methods (Hairer et al . 2002) correspond to bi-coloured trees.
leads to straightforward generalizations. For example, the P -series used in partitioned Runge-Kutta methods (Hairer et al . 2002) correspond to bi-coloured trees.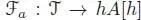 , such that ℱ a (•) = ha . It respects the gradings given by the number of vertices and the powers of h , respectively; hence, it extends to
, such that ℱ a (•) = ha . It respects the gradings given by the number of vertices and the powers of h , respectively; hence, it extends to  , where
, where  is the completion of
is the completion of 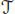 with respect to the grading. We further extend it to the empty tree by setting ∙ a(∅) = 1. We then have:
with respect to the grading. We further extend it to the empty tree by setting ∙ a(∅) = 1. We then have: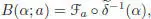
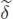 is the isomorphism from
is the isomorphism from 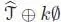 to
to  given by the normalized dual basis (see section 1.6.3).
given by the normalized dual basis (see section 1.6.3).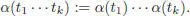
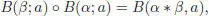
 and their character counterparts are identified modulo the above correspondence.
and their character counterparts are identified modulo the above correspondence. , which expresses itself as a B -series, that is,
, which expresses itself as a B -series, that is, 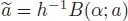 , where α is now a linear form on
, where α is now a linear form on 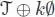 , such that α (∅) = 0. Here, we suppose that α (•) = 1. The following proposition is proven in Calaque et al . (2011):
, such that α (∅) = 0. Here, we suppose that α (•) = 1. The following proposition is proven in Calaque et al . (2011):