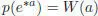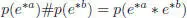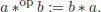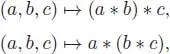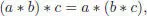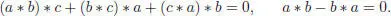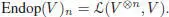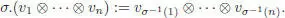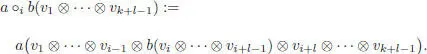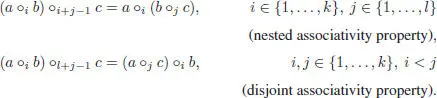[1.55] 
Suppose now that A is endowed with a complete decreasing compatible filtration as in section 1.4.2. This filtration induces a complete decreasing filtration S ( A ) = S ( A ) 0⊃ S ( A ) 1⊃ S ( A ) 2⊃ …, and the product * readily extends to the completion 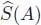 . For any a ∈ A , the application of equation [1.54]gives:
. For any a ∈ A , the application of equation [1.54]gives:
[1.56] 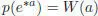
as an equality in the completed symmetric algebra 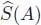 .
.
According to equation [1.48], we can identify the pro-unipotent group { e *a, a ∈ A } ⊂ 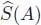 and the group of formal flows of the pre-Lie algebra A by means of the projection p , namely:
and the group of formal flows of the pre-Lie algebra A by means of the projection p , namely:
[1.57] 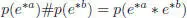
for any a, b ∈ A .
An operad is a combinatorial device which appeared in algebraic topology (May 1972), coined for coding “types of algebras”. Hence, for example, a Lie algebra is an algebra over some operad denoted by LIE, an associative algebra is an algebra over some operad denoted by ASSOC, a commutative algebra is an algebra over some operad denoted by COM and so on.
1.5.1. Manipulating algebraic operations
Algebra starts, in most cases, with some set E and some binary operation * : E × E → E . The set E shows some extra structure most of the time. Here, we will stick to the linear setting, where E is replaced by a vector space V (over some base field k ), and * is bilinear, that is, a linear map from V ⊗ V into V . A second bilinear map is deduced from the first by permuting the entries:
[1.58] 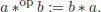
It also makes sense to look at tri-, quadri- and multi-linear operations, that is, linear maps from V ⊗nto V for any V . For example, it is very easy to produce 12 tri-linear maps starting with the bilinear map * by considering:
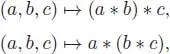
and the others deduced by permuting the three entries a , b and c . We could also introduce some tri- or multi-linear operations from scratch, that is, without deriving them from the bilinear operation *. We can even consider 1-ary and 0-ary operations, the latter being just distinguished elements of V . Note that there is a canonical 1-ary operation, namely, the identity map e : V → V . At this stage note that the symmetric group Sn obviously acts on the n -ary operations on the right by permuting the entries before composing them.
The bilinear operation * is not arbitrary in general: its properties determine the “type of algebra” considered. For example, V will be an associative or a Lie algebra if for any a, b, c ∈ V , we have respectively:
[1.59] 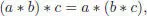
[1.60] 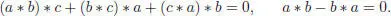
The concept of operad emerges when we try to rewrite such relations in terms of the operation * only, discarding the entries a, b, c . For example, the associativity axiom equation [1.59]informally expresses itself as follows: composing the operation * twice in two different ways gives the same result . Otherwise said:
[1.61] 
The Lie algebra axioms (equation [1.60]), involving flip and circular permutations, are clearly rewritten as:
[1.62] 
where τ is the flip (21) and σ is the circular permutation (231). The next section will give a precise meaning to these “partial compositions”, and we will end up giving the axioms of an operad, which is the natural framework in which equations like [1.61]and [1.62]make sense.
1.5.2. The operad of multi-linear operations
Let us now look at the prototype of algebraic operads: for any vector space V , the operad Endop( V ) is given by:
[1.63] 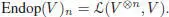
The right action of the symmetric group Sn on Endop( V ) nis induced by the left action of Sn on V ⊗ngiven by:
[1.64] 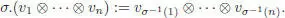
Elements of Endop( V ) nare conveniently represented as boxes with n inputs and one output: as illustrated by the graphical representation below, the partial composition a ∘ i b is given by:
[1.65] 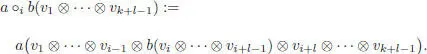
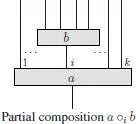
The following result is straightforward:
PROPOSITION 1.13.– For any a ∈ Endop( V ) k, b ∈ Endop( V ) land c ∈ Endop( V ) m, we have:
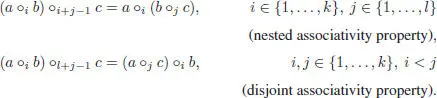
The identity e : V → V satisfies the following unit property :
[1.66] 
Читать дальше

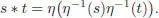
 . For any a ∈ A , the application of equation [1.54]gives:
. For any a ∈ A , the application of equation [1.54]gives: