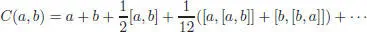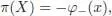
we get:
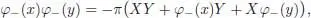
hence:
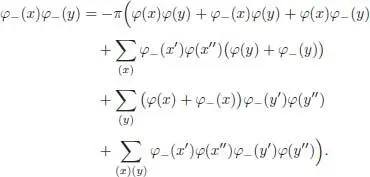
We have to compare this expression with:
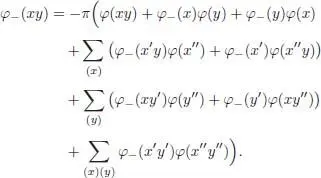
These two expressions are easily seen to be equal using the commutativity of the algebra 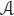 , the character property for φ and the induction hypothesis. □
, the character property for φ and the induction hypothesis. □
REMARK 1.2.– Assertion 2 admits a more conceptual proof (see the notes by Ebrahimi-Fard in the present volume), which is based on the following recursive expressions for the components of the Birkhoff decomposition: define the Bogoliubov preparation map as the map b : , recursively given by:
[1.34] 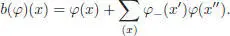
Then, the components of φ in the Birkhoff decomposition read :
[1.35] 
The Bogoliubov preparation map also writes in a more concise form :
[1.36] 
Plugging equation [1.36] into equation [1.35] and setting α := e − φ , we get the following expression for φ −:
[1.37] 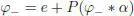
[1.38] 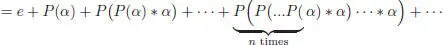
where 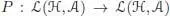 is the projection defined by P ( α ) = π ∘ α . The renormalizedpart φ+ satisfies an analogous recursive expression:
is the projection defined by P ( α ) = π ∘ α . The renormalizedpart φ+ satisfies an analogous recursive expression:
[1.39] 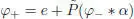
[1.40] 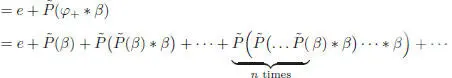
with β := φ 1* α = e – φ 1, and where is the projection on 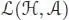 defined by
defined by 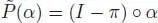 .
.
Pre-Lie algebras are sometimes called Vinberg algebras , as they appear in the work of Vinberg (1963) under the name “left-symmetric algebras” on the classification of homogeneous cones. They appear independently at the same time in the work of Gerstenhaber (1963) on Hochschild cohomology and deformations of algebras, under the name “pre-Lie algebras”, which is now the standard terminology. The term “chronological algebras” has also been used sometimes, for example, in the fundamental work of Agrachev and Gamkrelidze (1981). The notion itself can, however, be traced back to the work of Cayley (1857) which, in modern language, describes the pre-Lie algebra morphism Fa from the pre-Lie algebra of rooted trees into the pre-Lie algebra of vector fields on ℝ n, sending the one-vertex tree to a given vector field a . For a survey emphasizing geometric aspects, see Burde (2006).
1.4.1. Definition and general properties
A left pre-Lie algebra over a field k is a k -vector space A with a bilinear binary composition ⊳ that satisfies the left pre-Lie identity:
[1.41] 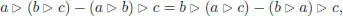
for a , b , c ∈ A . Analogously, a right pre-Lie algebra is a k -vector space A with a binary composition ⊲ that satisfies the right pre-Lie identity:
[1.42] 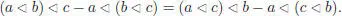
The left pre-Lie identity is rewritten as:
[1.43] 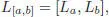
where La : A → A is defined by Lab = a ⊳ b , and the bracket on the left-hand side is defined by [ a, b ] := a ⊳ b – b ⊳ a . As an easy consequence, this bracket satisfies the Jacobi identity: If A is unital (i.e. there exists 1∈ A , such that 1⊳ a = a ⊳ 1= 1for any a ∈ A ), it is immediate thanks to the fact that L : A → End A is injective. If not, we can add a unit by considering 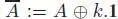 and extend
and extend 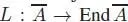 accordingly. As any right pre-Lie algebra ( A , ⊲) is also a left pre-Lie algebra with product a ⊳ b := b ⊲ a , we can stick to left pre-Lie algebras, which we will do unless specifically indicated.
accordingly. As any right pre-Lie algebra ( A , ⊲) is also a left pre-Lie algebra with product a ⊳ b := b ⊲ a , we can stick to left pre-Lie algebras, which we will do unless specifically indicated.
1.4.2. The group of formal flows
The following is taken from the paper by Agrachev and Gamkrelidze (1981). Suppose that A is a left pre-Lie algebra endowed with a compatible decreasing filtration, namely, A = A 1⊃ A 2⊂ A 3⊃ …, such that the intersection of the Aj ’s reduces to {0}, and such that Ap ⊳ Aq ⊂ A p+q. Suppose, moreover, that A is complete with respect to this filtration. The Baker-Campbell-Hausdorff formula:
[1.44] 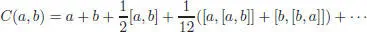
Читать дальше

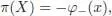
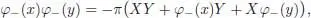
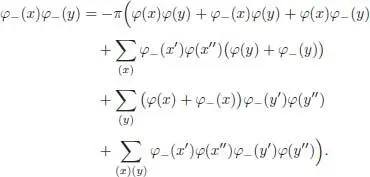
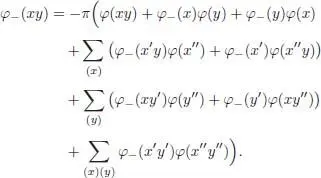
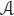 , the character property for φ and the induction hypothesis. □
, the character property for φ and the induction hypothesis. □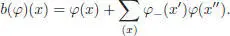


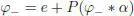
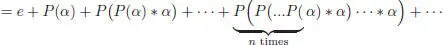
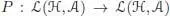 is the projection defined by P ( α ) = π ∘ α . The renormalizedpart φ+ satisfies an analogous recursive expression:
is the projection defined by P ( α ) = π ∘ α . The renormalizedpart φ+ satisfies an analogous recursive expression: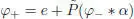
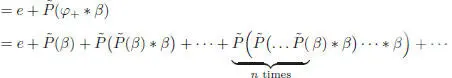
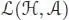 defined by
defined by 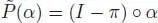 .
.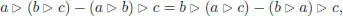
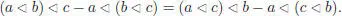
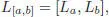
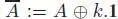 and extend
and extend 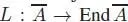 accordingly. As any right pre-Lie algebra ( A , ⊲) is also a left pre-Lie algebra with product a ⊳ b := b ⊲ a , we can stick to left pre-Lie algebras, which we will do unless specifically indicated.
accordingly. As any right pre-Lie algebra ( A , ⊲) is also a left pre-Lie algebra with product a ⊳ b := b ⊲ a , we can stick to left pre-Lie algebras, which we will do unless specifically indicated.