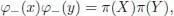1 ...8 9 10 12 13 14 ...24 PROPOSITION 1.12.–
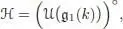
where is the Lie algebra of infinitesimal characters with values in the base field k, where stands for its enveloping algebra, and (—)° stands for the graded dual .
In the case when the Hopf algebra ℋ is not commutative, it is no longer possible to reconstruct it from G 1( k ).
1.3.7. Renormalization in connected filtered Hopf algebras
In this section we describe the renormalization à la Connes-Kreimer (Connes and Kreimer 1998; Kreimer 2002) in the abstract context of connected filtered Hopf algebras: the objects to be renormalized are characters with values in a commutative unital target algebra  endowed with a renormalization scheme , that is, a splitting
endowed with a renormalization scheme , that is, a splitting  into two subalgebras. An important example is given by the minimal subtraction scheme of the algebra
into two subalgebras. An important example is given by the minimal subtraction scheme of the algebra  of meromorphic functions of one variable z , where
of meromorphic functions of one variable z , where  is the algebra of meromorphic functions which are holomorphic at z = 0, and
is the algebra of meromorphic functions which are holomorphic at z = 0, and 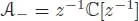 stands for the “polar parts”. Any
stands for the “polar parts”. Any  -valued character φ admits a unique Birkhoff decomposition :
-valued character φ admits a unique Birkhoff decomposition :
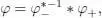
where φ +is an 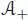 -valued character, and φ (Ker ε ) ⊂
-valued character, and φ (Ker ε ) ⊂ 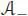 . In the MS scheme case described above, the renormalized character is the scalar-valued character given by the evaluation of φ +at z = 0 (whereas the evaluation of φ at z = 0 does not necessarily make sense).
. In the MS scheme case described above, the renormalized character is the scalar-valued character given by the evaluation of φ +at z = 0 (whereas the evaluation of φ at z = 0 does not necessarily make sense).
Here, we consider the situation where the algebra  admits a renormalization scheme , that is, a splitting into two subalgebras:
admits a renormalization scheme , that is, a splitting into two subalgebras:
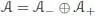
with 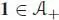 . Let
. Let  be the projection on
be the projection on 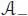 parallel to
parallel to 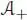 .
.
THEOREM 1.2.–
1 1) Let ℋ be a connected filtered Hopf algebra. Let be the group of those , such that endowed with the convolution product. Any admits a unique Birkhoff decomposition:
[1.30] 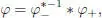
where φ− sends 1 to and Ker ε into , and φ+ sends ℋ into . The maps φ -and φ + are given on Ker ε by the following recursive formulae :
[1.31] 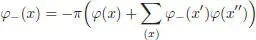
[1.32] 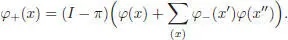
1 2) If the algebra is commutative and if φ is a character, the components φ- and φ+ occurring in the Birkhoff decomposition of χ are characters as well.
PROOF .– The proof goes along the same lines as the proof of Theorem 4 from Connes and Kreimer (1998): for the first assertion, it is immediate from the definition of π that φ -sends Ker ε into 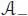 , and that φ +sends Ker ε into
, and that φ +sends Ker ε into 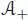 . It only remains to check equality φ += φ -* φ , which is an easy computation:
. It only remains to check equality φ += φ -* φ , which is an easy computation:
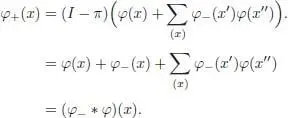
The proof of assertion 2 goes exactly as in Connes and Kreimer (1998) and relies on the following Rota–Baxter relation in  :
:
[1.33] 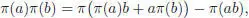
which is easily verified by decomposing a and b into their 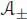 -parts. Let φ be a character of ℋ with values in
-parts. Let φ be a character of ℋ with values in  . Suppose that we have φ -( xy ) = φ -( x ) φ − ( y ) for any x, y ∈ ℋ, such that | x | + | y | ≤ d – 1, and compute for x , y , such that | x | + | y | = d :
. Suppose that we have φ -( xy ) = φ -( x ) φ − ( y ) for any x, y ∈ ℋ, such that | x | + | y | ≤ d – 1, and compute for x , y , such that | x | + | y | = d :
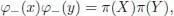
with X = φ ( x ) – Σ (x) φ -( x ′) φ ( x ″) and Y = φ ( y ) – Σ (y) φ – ( y ′) φ ( y ″). Using the formula:
Читать дальше

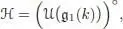
 endowed with a renormalization scheme , that is, a splitting
endowed with a renormalization scheme , that is, a splitting  into two subalgebras. An important example is given by the minimal subtraction scheme of the algebra
into two subalgebras. An important example is given by the minimal subtraction scheme of the algebra 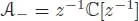 stands for the “polar parts”. Any
stands for the “polar parts”. Any 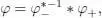
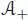 -valued character, and φ (Ker ε ) ⊂
-valued character, and φ (Ker ε ) ⊂ 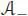 . In the MS scheme case described above, the renormalized character is the scalar-valued character given by the evaluation of φ +at z = 0 (whereas the evaluation of φ at z = 0 does not necessarily make sense).
. In the MS scheme case described above, the renormalized character is the scalar-valued character given by the evaluation of φ +at z = 0 (whereas the evaluation of φ at z = 0 does not necessarily make sense).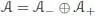
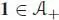 . Let
. Let  be the projection on
be the projection on 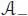 parallel to
parallel to 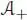 .
.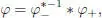
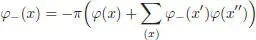
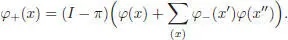
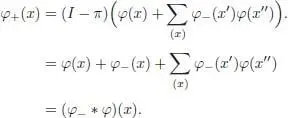
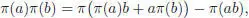
 -parts. Let φ be a character of ℋ with values in
-parts. Let φ be a character of ℋ with values in