5Departamento de Matemática, Instituto de Ciências Exatas, Universidade Federal de Juiz de Fora, Juiz de Fora, MG, Brazil
This preliminary chapter is devoted to two pillars of the theory of generalized ordinary differential equations for which we use the short form “generalized ODEs” . One of these pillars concerns the spaces in which the solutions of a generalized ODE are generally placed. The other pillar concerns the theory of nonabsolute integration, due to Jaroslav Kurzweil and Ralph Henstock, for integrands taking values in Banach spaces. As a matter of fact, such integration theory permeates the entire book. It (the theory of non absolute integration) is within the heartwood of the theory of generalized ODEs, appearing (the same theory of nonabsolute integration) in the integral form of a very special case of nonautonomous generalized ODEs, namely (now we mention the name of the special case of generalized ODEs), measure functional differential equations.
The solutions of a Cauchy problem for a generalized ODE, with right‐hand side in a class of functions introduced by J. Kurzweil in [147–149], usually belong to a certain space of functions of bounded variation (see Lemma 4.9). However, since functions of bounded variation are also regulated functions in the sense described by Jean Dieudonné and, more generally, by the group Nicolas Bourbaki, and because the space of regulated functions is more adequate for dealing with discontinuous functions appearing naturally in Stieltjes‐type integrals, it is important to present a substantial content about this space. Thus, the first section of this chapter describes the main properties of the space of regulated functions with the icing of the cake being a characterization of its relatively compact subsets due to D. Franková.
Regarding functions of bounded variation, which are known to be of bounded semivariation and, hence, of bounded 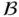 ‐variation, we present, in the second section of this chapter, a coherent overview of functions of bounded
‐variation, we present, in the second section of this chapter, a coherent overview of functions of bounded 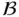 ‐variation over bilinear triples. Among the results involving functions of bounded variation, the theorem of Helly (or the Helly's choice principle for Banach space‐valued function) due to C. S. Hönig is a spotlight. On the other hand, functions of bounded semivariation appear, for instance, in the integration by parts formula for Kurzweil and Henstock integrals of Stieltjes‐type.
‐variation over bilinear triples. Among the results involving functions of bounded variation, the theorem of Helly (or the Helly's choice principle for Banach space‐valued function) due to C. S. Hönig is a spotlight. On the other hand, functions of bounded semivariation appear, for instance, in the integration by parts formula for Kurzweil and Henstock integrals of Stieltjes‐type.
In the third section of this chapter, we describe the second pillar and main background of the theory of generalized ODEs, namely, the framework of vector‐valued nonabsolute integrals of Kurzweil and Henstock. Here, we call the reader's attention to the fact that we refer to Kurzweil vector integrals as Perron–Stieltjes integrals so that, when a more general definition of the Kurzweil integral is presented in Chapter 1, the reader will not be confused. One of the highlights of the third section is, then, the integration by parts formula for Perron–Stieltjes integrals.
An extra section called “Appendix,” which can be skipped in a first reading of the book, concerns other types of gauge‐based integrals which use the interesting idea of Edward James McShane. The well‐known Bochner–Lebesgue integral comes into the scene and an equivalent definition of it as the limit of Riemannian‐type sums comes up.
Regulated functions appear in the works by J. Dieudonné [58, p. 139] and N. Bourbaki [32, p. II.4]. The raison d'être of regulated functions lies on the fact that every regulated function 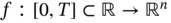 has a primitive, that is, there exists a continuous function
has a primitive, that is, there exists a continuous function  such that
such that 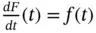 almost everywhere in
almost everywhere in 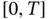 , in the sense of the Lebesgue measure. The interested reader may want to check this fact as described, for instance, by the group N. Bourbaki in [32, Corollaire I, p. II.6].
, in the sense of the Lebesgue measure. The interested reader may want to check this fact as described, for instance, by the group N. Bourbaki in [32, Corollaire I, p. II.6].
Let 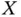 be a Banach space with norm
be a Banach space with norm 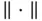 . Here, we describe regulated functions
. Here, we describe regulated functions 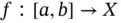 , where
, where 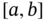 , with
, with 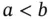 , is a compact interval of the real line
, is a compact interval of the real line 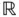 .
.
Definition 1.1:A function 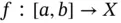 is called regulated , if the lateral limits
is called regulated , if the lateral limits
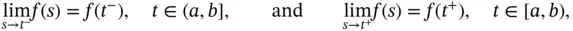
exist. The space of all regulated functions 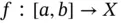 will be denoted by
will be denoted by 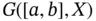 .
.
We denote the subspace of all continuous functions 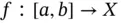 by
by 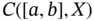 and, by
and, by 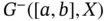 , we mean the subspace of regulated functions
, we mean the subspace of regulated functions 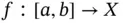 which are left‐continuous on
which are left‐continuous on 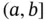 . Then, the following inclusions clearly hold
. Then, the following inclusions clearly hold
Читать дальше

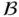 ‐variation, we present, in the second section of this chapter, a coherent overview of functions of bounded
‐variation, we present, in the second section of this chapter, a coherent overview of functions of bounded 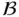 ‐variation over bilinear triples. Among the results involving functions of bounded variation, the theorem of Helly (or the Helly's choice principle for Banach space‐valued function) due to C. S. Hönig is a spotlight. On the other hand, functions of bounded semivariation appear, for instance, in the integration by parts formula for Kurzweil and Henstock integrals of Stieltjes‐type.
‐variation over bilinear triples. Among the results involving functions of bounded variation, the theorem of Helly (or the Helly's choice principle for Banach space‐valued function) due to C. S. Hönig is a spotlight. On the other hand, functions of bounded semivariation appear, for instance, in the integration by parts formula for Kurzweil and Henstock integrals of Stieltjes‐type.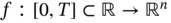 has a primitive, that is, there exists a continuous function
has a primitive, that is, there exists a continuous function  such that
such that 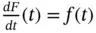 almost everywhere in
almost everywhere in 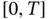 , in the sense of the Lebesgue measure. The interested reader may want to check this fact as described, for instance, by the group N. Bourbaki in [32, Corollaire I, p. II.6].
, in the sense of the Lebesgue measure. The interested reader may want to check this fact as described, for instance, by the group N. Bourbaki in [32, Corollaire I, p. II.6].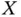 be a Banach space with norm
be a Banach space with norm 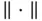 . Here, we describe regulated functions
. Here, we describe regulated functions 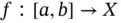 , where
, where 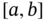 , with
, with 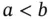 , is a compact interval of the real line
, is a compact interval of the real line 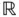 .
.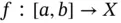 is called regulated , if the lateral limits
is called regulated , if the lateral limits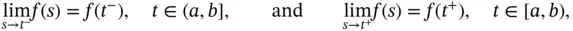
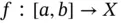 will be denoted by
will be denoted by 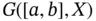 .
.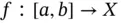 by
by 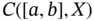 and, by
and, by 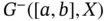 , we mean the subspace of regulated functions
, we mean the subspace of regulated functions 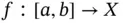 which are left‐continuous on
which are left‐continuous on 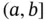 . Then, the following inclusions clearly hold
. Then, the following inclusions clearly hold










