Nevertheless, it was only in 2002 that the theory really started to be developed here. The article by Professors Márcia Federson and Plácido Táboas, published in the Journal of Differential Equations in 2003 (see [92]), was the first Brazilian publication on the subject. Now, 18 years later, members of the Brazilian research group on Functional Differential Equations and Nonabsolute Integration decided to gather the results obtained over these years in order to produce a comprehensive literature about our results developed so far, regarding the theory of generalized ODEs in abstract spaces.
Originally, this monograph was thought to be organized by professors Márcia Federson, Everaldo M. Bonotto, and Jaqueline G. Mesquita, with the contribution of the following authors: Suzete M. Afonso, Fernando G. Andrade, Fernanda Andrade da Silva, Marielle Ap. Silva, Rodolfo Collegari, Miguel Frasson, Luciene P. Gimenes, Rogelio Grau, Maria Carolina Mesquita, Patricia H. Tacuri, and Eduard Toon. However, after a while, it became a production of us all, with contributions of everyone to all chapters and to the uniformity, coherence, language, and interrelationship of the results. We, then, present this carefully crafted work to disseminate the theories involved here, especially those on Kurzweil–Henstock nonabsolute integration and on generalized ODEs.
In the introductory chapter, named Preliminaries , we brought together two main issues that permeate this book. The first one concerns the spaces where the functions within the right-hand sides of differential or integral equations live. The other one concerns the theory of nonabsolute vector-valued integrals in the senses of J. Kurzweil and R. Henstock. Sections 1.1and 1.2are devoted to properties of the space of regulated functions and the space of functions of bounded 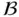 -variation. Among the main results of Section 1.1, we mention a characterization, based on [96, 97], of relatively compact sets of the space of regulated functions. Section 1.2deals with properties of functions of bounded
-variation. Among the main results of Section 1.1, we mention a characterization, based on [96, 97], of relatively compact sets of the space of regulated functions. Section 1.2deals with properties of functions of bounded 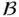 -variation where the Helly's choice principle for abstract spaces is a spotlight. The book [127] is the main reference for this section. The third section is devoted to nonabsolute vector-valued integrals. The basis of this theory is presented here and results specialized for Perron–Stieltjes integrals are included. We highlight substitution formulas and an integration by parts formula coming from [212]. Other important references to this section are [72, 73, 210].
-variation where the Helly's choice principle for abstract spaces is a spotlight. The book [127] is the main reference for this section. The third section is devoted to nonabsolute vector-valued integrals. The basis of this theory is presented here and results specialized for Perron–Stieltjes integrals are included. We highlight substitution formulas and an integration by parts formula coming from [212]. Other important references to this section are [72, 73, 210].
The second chapter is devoted to the integral as defined by Jaroslav Kurzweil in [147]. We compiled some historical data on how the idea of the integral came about. Highlights of this chapter include the Saks–Henstock lemma, the Hake-type theorem, and the change of variables theorem. We end this chapter with a brief history of the Kapitza pendulum equation whose solution is highly oscillating and, therefore, suitable for being treated via Kurzweil–Henstock nonabsolute integration theory. An important reference to Chapter 2is [209].
Before entering the theory of generalized ODEs, we take a trip through the theory of measure functional differential equations (we write measure FDEs for short). Then, the third chapter appears as an embracing collection of results on measure FDEs for Banach space-valued functions. In particular, we investigate equations of the form
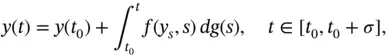
where 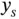 is a memory function and the integral on the right-hand side is in the sense of Perron–Stieltjes. We show that these equations encompass not only impulsive functional dynamic equations on time scales but also impulsive measure FDEs. Examples illustrating the relations between any two of these equations are also included. References [85, 86] feature as the foundation for this relations. Among other topics covered by Chapter 3, we mention averaging principles, covering the periodic and nonperiodic cases, and results on continuous dependence of solutions on time scales. References [21, 82, 178] are crucial here.
is a memory function and the integral on the right-hand side is in the sense of Perron–Stieltjes. We show that these equations encompass not only impulsive functional dynamic equations on time scales but also impulsive measure FDEs. Examples illustrating the relations between any two of these equations are also included. References [85, 86] feature as the foundation for this relations. Among other topics covered by Chapter 3, we mention averaging principles, covering the periodic and nonperiodic cases, and results on continuous dependence of solutions on time scales. References [21, 82, 178] are crucial here.
In Chapter 4, we enter the theory of generalized ODE itself. We begin by recalling the concept of a nonautonomous generalized ODE of the form
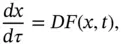
where 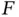 takes a pair
takes a pair 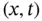 of a regulated function
of a regulated function 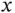 and a time
and a time 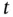 to a regulated function. The main reference to this chapter is [209]. Measure FDEs in the integral form described above feature in Chapter 4as supporting actors, because now their solutions can be related to solutions of the generalized ODEs, whose right-hand sides involve functions which look like
to a regulated function. The main reference to this chapter is [209]. Measure FDEs in the integral form described above feature in Chapter 4as supporting actors, because now their solutions can be related to solutions of the generalized ODEs, whose right-hand sides involve functions which look like
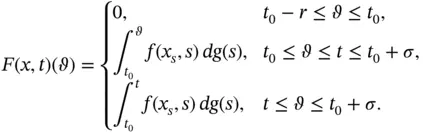
This characteristic of generalized ODEs plays an important role in the entire manuscript, since it allows one to translate results from generalized ODEs to measure FDEs.
Chapter 5, based on [78], brings together the foundations of the theory of generalized ODEs. Section 5.1 concerns local existence and uniqueness of a solution of a nonautonomous generalized ODE with applications to measure FDEs and functional dynamic equations on time scales. Second 5.2 is devoted to results on prolongation of solutions of generalized ODEs, measure differential equations, and dynamic equations on time scales.
Chapter 6deals with a very important class of differential equations, the class of linear generalized ODEs. The origins of linear generalized ODEs goes back to the papers [209–211]. Here, we recall the notion of fundamental operator associated with a linear generalized ODE for Banach space-valued functions and we travel on the same road as the authors of [45] to obtain a variation-of-constants formula for a linear perturbed generalized ODE. Concerning applications, we extend the class of equations to include linear measure FDEs.
After linear generalized ODEs are investigated, we move to results on continuous dependence of solutions on parameters. This is the core of Chapter 7which is based on [4, 95, 96, 177]. Given a family of generalized ODEs, we present sufficient conditions so that the family of their corresponding solutions converge uniformly, on compact sets, to the solution of the limiting generalized ODE. We also prove that given a generalized ODE and its solution 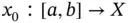 , where
, where 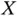 is a Banach space, one can obtain a family of generalized ODEs whose solutions converge uniformly to
is a Banach space, one can obtain a family of generalized ODEs whose solutions converge uniformly to 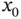 on
on 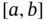 .
.
Читать дальше

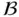 -variation. Among the main results of Section 1.1, we mention a characterization, based on [96, 97], of relatively compact sets of the space of regulated functions. Section 1.2deals with properties of functions of bounded
-variation. Among the main results of Section 1.1, we mention a characterization, based on [96, 97], of relatively compact sets of the space of regulated functions. Section 1.2deals with properties of functions of bounded 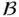 -variation where the Helly's choice principle for abstract spaces is a spotlight. The book [127] is the main reference for this section. The third section is devoted to nonabsolute vector-valued integrals. The basis of this theory is presented here and results specialized for Perron–Stieltjes integrals are included. We highlight substitution formulas and an integration by parts formula coming from [212]. Other important references to this section are [72, 73, 210].
-variation where the Helly's choice principle for abstract spaces is a spotlight. The book [127] is the main reference for this section. The third section is devoted to nonabsolute vector-valued integrals. The basis of this theory is presented here and results specialized for Perron–Stieltjes integrals are included. We highlight substitution formulas and an integration by parts formula coming from [212]. Other important references to this section are [72, 73, 210].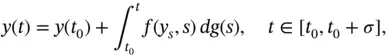
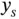 is a memory function and the integral on the right-hand side is in the sense of Perron–Stieltjes. We show that these equations encompass not only impulsive functional dynamic equations on time scales but also impulsive measure FDEs. Examples illustrating the relations between any two of these equations are also included. References [85, 86] feature as the foundation for this relations. Among other topics covered by Chapter 3, we mention averaging principles, covering the periodic and nonperiodic cases, and results on continuous dependence of solutions on time scales. References [21, 82, 178] are crucial here.
is a memory function and the integral on the right-hand side is in the sense of Perron–Stieltjes. We show that these equations encompass not only impulsive functional dynamic equations on time scales but also impulsive measure FDEs. Examples illustrating the relations between any two of these equations are also included. References [85, 86] feature as the foundation for this relations. Among other topics covered by Chapter 3, we mention averaging principles, covering the periodic and nonperiodic cases, and results on continuous dependence of solutions on time scales. References [21, 82, 178] are crucial here.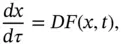
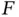 takes a pair
takes a pair 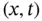 of a regulated function
of a regulated function 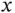 and a time
and a time 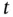 to a regulated function. The main reference to this chapter is [209]. Measure FDEs in the integral form described above feature in Chapter 4as supporting actors, because now their solutions can be related to solutions of the generalized ODEs, whose right-hand sides involve functions which look like
to a regulated function. The main reference to this chapter is [209]. Measure FDEs in the integral form described above feature in Chapter 4as supporting actors, because now their solutions can be related to solutions of the generalized ODEs, whose right-hand sides involve functions which look like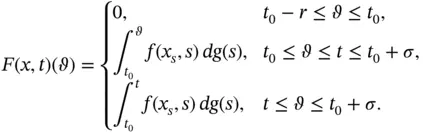
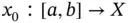 , where
, where 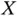 is a Banach space, one can obtain a family of generalized ODEs whose solutions converge uniformly to
is a Banach space, one can obtain a family of generalized ODEs whose solutions converge uniformly to 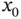 on
on 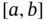 .
.










