As we mentioned before, many types of differential equations can be regarded as generalized ODEs. This fact allows us to derive stability results for these equations through the relations between the solutions of a certain equations and the solutions of a generalized ODEs. At the present time, the stability theory for generalized ODEs is undergoing a remarkable development. Recent results in this respect are contained in [3, 7, 80, 89, 90] and are gathered in Chapter 8. We also show the effectiveness of Lyapunov's Direct Method to obtain several stability results, in addition to proving converse Lyapunov theorems for some types of stability. The types of stability explore here are variational stability, Lyapunov stability, regular stability, and many relations permeating these concepts.
The existence of periodic solutions to any kind of equation is also of great interest, especially in applications. Chapter 9is devoted to this matter in the framework of generalized ODEs, whose results are also specified to measure differential equations and impulsive differential equations. Section 9.1 brings together a result which provides conditions for the solutions of a linear generalized ODE taking values in 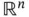 to be periodic and a result which relates periodic solutions of linear nonhomogeneous generalized ODEs to periodic solutions of linear homogeneous generalized ODEs. Still in this section, a characterization of the fundamental matrix of periodic linear generalized ODEs is established. This is the analogue of the Floquet theorem for generalized ODEs involving finite dimensional space-valued functions. In Section 9.2, inspired in an approach by Jean Mawhin to treat periodic boundary value problem (we write periodic BVP for short), we introduce the concept of a
to be periodic and a result which relates periodic solutions of linear nonhomogeneous generalized ODEs to periodic solutions of linear homogeneous generalized ODEs. Still in this section, a characterization of the fundamental matrix of periodic linear generalized ODEs is established. This is the analogue of the Floquet theorem for generalized ODEs involving finite dimensional space-valued functions. In Section 9.2, inspired in an approach by Jean Mawhin to treat periodic boundary value problem (we write periodic BVP for short), we introduce the concept of a 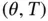 -periodic solution for a nonlinear homogeneous generalized ODE in Banach spaces, where
-periodic solution for a nonlinear homogeneous generalized ODE in Banach spaces, where 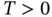 and
and 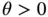 . A result that ensures a correspondence between solutions of a
. A result that ensures a correspondence between solutions of a 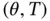 -periodic BVP and
-periodic BVP and 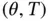 -periodic solutions of a nonlinear homogeneous generalized ODE is the spotlight here. Then, the existence of a
-periodic solutions of a nonlinear homogeneous generalized ODE is the spotlight here. Then, the existence of a 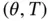 -periodic solution is guaranteed.
-periodic solution is guaranteed.
Averaging methods are used to investigate the solutions of a nonautonomous differential equations by means of the solutions of an “ averaged ” autonomous equation. In Chapter 10, we present a periodic averaging principle as well as a nonperiodic one for generalized ODEs. The main references to this chapter are [83, 178].
Chapter 11is designed to provide the reader with a systematic account of recent developments in the boundedness theory for generalized ODEs. The results of this chapter were borrowed from the articles [2, 79].
Chapter 12is devoted to the control theory in the setting of abstract generalized ODEs. In its first section, we introduce concepts of observability, exact controllability, and approximate controllability, and we give necessary and sufficient conditions for a system of generalized ODEs to be exactly controllable, approximately controllable, or observable. In Section 12.2, we apply the results to classical ODEs.
The study of exponential dichotomy for linear generalized ODEs of type
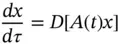
is the heartwood of Chapter 13, where sufficient conditions for the existence of exponential dichotomies are obtained, as well as conditions for the existence of bounded solutions for the nonhomogeneous equation
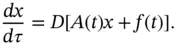
Using the relations between the solutions of generalized ODEs and the solutions of other types of equations, we translate our results to measure differential equations and impulsive differential equations. The main reference for this chapter is [29].
The aim of Chapter 14is to bring together the theory of semidynamical systems generated by generalized ODEs. We show the existence of a local semidynamical system generated by a nonautonomous generalized ODE of the form
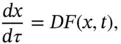
where 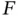 belongs to a compact class of right-hand sides. We construct an impulsive semidynamical system associated with a generalized ODE subject to external impulse effects. For this class of impulsive systems, we present a LaSalle's invariance principle-type result. Still in this chapter, we present some topological properties for impulsive semidynamical systems as minimality and recurrence. The main reference here is [4].
belongs to a compact class of right-hand sides. We construct an impulsive semidynamical system associated with a generalized ODE subject to external impulse effects. For this class of impulsive systems, we present a LaSalle's invariance principle-type result. Still in this chapter, we present some topological properties for impulsive semidynamical systems as minimality and recurrence. The main reference here is [4].
Chapter 15is intended for applications of the theory developed in some of the previous chapters to a class of more general functional differential equations, namely, measure FDE of neutral type. In Section 15.1, some historical notes ranging from the beginnings of the term equation , passing through “ functional differential equation ,” and reaching functional differential equation of neutral type are put together. Then, we present a correspondence between solutions of a measure FDE of neutral type with finite delays and solutions of a generalized ODEs. Results on existence and uniqueness of a solution as well as continuous dependence of solutions on parameters based on [76] are also explored.
We end this preface by expressing our immense gratitude to professors Jaroslav Kurzweil, Štefan Schwabik ( in memorian ) and Milan Tvrdý for welcoming several members of our research group at the Institute of Mathematics of the Academy of Sciences of the Czech Republic so many times, for the countably many good advices and talks, and for the corrections of proofs and theorems during all these years.
October 2020
Everaldo M. Bonotto
Márcia Federson
Jaqueline G. Mesquita
São Carlos, SP, Brazil
Everaldo M. Bonotto1, Rodolfo Collegari2, Márcia Federson3, Jaqueline G. Mesquita4, and Eduard Toon5
1Departamento de Matemática Aplicada e Estatística, Instituto de Ciências Matemáticas e de Computação (ICMC), Universidade de São Paulo, São Carlos, SP, Brazil
2Faculdade de Matemática, Universidade Federal de Uberlândia, Uberlândia, MG, Brazil
3Departamento de Matemática, Instituto de Ciências Matemáticas e de Computação (ICMC), Universidade de São Paulo, São Carlos, SP, Brazil
4Departamento de Matemática, Instituto de Ciências Exatas, Universidade de Brasília, Brasília, DF, Brazil
Читать дальше

 to be periodic and a result which relates periodic solutions of linear nonhomogeneous generalized ODEs to periodic solutions of linear homogeneous generalized ODEs. Still in this section, a characterization of the fundamental matrix of periodic linear generalized ODEs is established. This is the analogue of the Floquet theorem for generalized ODEs involving finite dimensional space-valued functions. In Section 9.2, inspired in an approach by Jean Mawhin to treat periodic boundary value problem (we write periodic BVP for short), we introduce the concept of a
to be periodic and a result which relates periodic solutions of linear nonhomogeneous generalized ODEs to periodic solutions of linear homogeneous generalized ODEs. Still in this section, a characterization of the fundamental matrix of periodic linear generalized ODEs is established. This is the analogue of the Floquet theorem for generalized ODEs involving finite dimensional space-valued functions. In Section 9.2, inspired in an approach by Jean Mawhin to treat periodic boundary value problem (we write periodic BVP for short), we introduce the concept of a 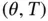 -periodic solution for a nonlinear homogeneous generalized ODE in Banach spaces, where
-periodic solution for a nonlinear homogeneous generalized ODE in Banach spaces, where 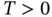 and
and 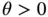 . A result that ensures a correspondence between solutions of a
. A result that ensures a correspondence between solutions of a 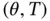 -periodic BVP and
-periodic BVP and 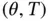 -periodic solutions of a nonlinear homogeneous generalized ODE is the spotlight here. Then, the existence of a
-periodic solutions of a nonlinear homogeneous generalized ODE is the spotlight here. Then, the existence of a 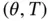 -periodic solution is guaranteed.
-periodic solution is guaranteed.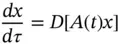
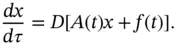
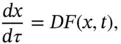
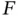 belongs to a compact class of right-hand sides. We construct an impulsive semidynamical system associated with a generalized ODE subject to external impulse effects. For this class of impulsive systems, we present a LaSalle's invariance principle-type result. Still in this chapter, we present some topological properties for impulsive semidynamical systems as minimality and recurrence. The main reference here is [4].
belongs to a compact class of right-hand sides. We construct an impulsive semidynamical system associated with a generalized ODE subject to external impulse effects. For this class of impulsive systems, we present a LaSalle's invariance principle-type result. Still in this chapter, we present some topological properties for impulsive semidynamical systems as minimality and recurrence. The main reference here is [4].










