Mohammad Asadzadeh - An Introduction to the Finite Element Method for Differential Equations

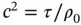Letting and 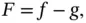we end up with the following concise form: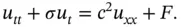

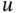(1.5.28)

Equation ( 1.5.28) describes the vibration of the considered string once it is set into motion. The smallness assumption here results in a single linear equation for . Due to the presence of the friction term 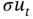, Eq. (1.5.28)is often referred to as the damped one‐dimensional wave equation . If friction is negligible, then we can let 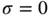and get the inhomogeneous wave equation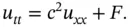

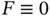(1.5.29)

In the absence of external forces and when the weight of the string is negligible, we may take to get the one‐dimensional wave equation :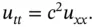

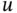(1.5.30)

Note that since has the unit of length 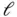, 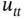has the unit of acceleration and 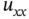the unit of 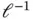, hence, 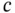has the unit of velocity.

1 Problem 1.8 Show that satisfies Laplace's equation for .

2 Problem 1.9 Show that satisfies Laplace's equation , for .

3 Problem 1.10 Show that satisfies the Laplace equation in polar coordinates:

4 Problem 1.11 Verify thatboth satisfy the Laplace equation, and sketch the curves constant and constant. Show that

5 Problem 1.12 Show that satisfies the heat equation for .

6 Problem 1.13 Show that satisfies the heat equation , for .

7 Problem 1.14 The spherically symmetric form of the heat conduction equation is given byShow that satisfies the standard one‐dimensional heat equation.

8 Problem 1.15 Show that the equationcan be reduced to the standard heat conduction equation by writing . How do you interpret the term ?

9 Problem 1.16 Use the substitution to transform the one‐dimensional convection–diffusion equationinto a heat equation for .

10 Problem 1.17 If , let satisfyDerive the identity

11 Problem 1.18 Find the possible values of and in the expression such that it satisfies the wave equation

12 Problem 1.19 Taking , where is any function, find the values of that will ensure satisfies the wave equation

13 Problem 1.20 The spherically symmetric version of the wave equation takes the formShow, by putting , that it has a solution of the form

14 Problem 1.21 Let and . Use the chain rule to show that

15 Problem 1.22 Show that the solution of the initial value problemsatisfies d'Alembert's formula:

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.