(1.5.4) 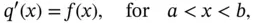
which expresses conservation of energy in differential equation form. We need an additional equation that relates the heat flux 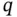 to the temperature gradient
to the temperature gradient 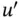 called a constitutive equation. The simplest constitutive equation for heat flow is Fourier's law :
called a constitutive equation. The simplest constitutive equation for heat flow is Fourier's law :
(1.5.5) 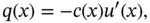
which states that heat flows from warm regions to cold regions at a rate proportional to the temperature gradient 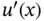 . The constant of proportionality is the coefficient of heat conductivity
. The constant of proportionality is the coefficient of heat conductivity 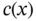 , which we assume to be a positive function in
, which we assume to be a positive function in 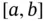 . Combining ( 1.5.4) and ( 1.5.5) gives the stationary heat equation in one dimension :
. Combining ( 1.5.4) and ( 1.5.5) gives the stationary heat equation in one dimension :
(1.5.6) 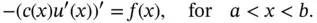
To define a solution 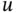 uniquely, the differential equation is complemented by boundary conditions imposed at the boundary points
uniquely, the differential equation is complemented by boundary conditions imposed at the boundary points 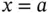 and
and 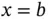 . A common example is the homogeneous Dirichlet conditions
. A common example is the homogeneous Dirichlet conditions 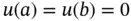 , corresponding to keeping the temperature at zero at the endpoints of the wire. The result is a two‐point BVP :
, corresponding to keeping the temperature at zero at the endpoints of the wire. The result is a two‐point BVP :
(1.5.7) 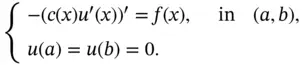
The boundary condition 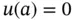 may be replaced by
may be replaced by 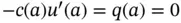 , corresponding to prescribing zero heat flux, or insulating the wire, at
, corresponding to prescribing zero heat flux, or insulating the wire, at 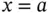 . Later, we also consider nonhomogeneous boundary conditions of the form
. Later, we also consider nonhomogeneous boundary conditions of the form 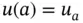 or
or 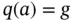 where
where 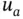 and
and 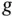 may be different from zero. For other types of boundary conditions, see Trinities ( Section 1.2).
may be different from zero. For other types of boundary conditions, see Trinities ( Section 1.2).
The time‐dependent heat equation in ( 1.5.2) describes the diffusion of thermal energy in a homogeneous material, where 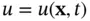 is the temperature at a position
is the temperature at a position 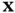 at time
at time 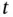 and
and 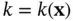 is called thermal diffusivity or heat conductivity (corresponding to
is called thermal diffusivity or heat conductivity (corresponding to 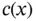 in ( 1.5.5)–( 1.5.7)) of the material.
in ( 1.5.5)–( 1.5.7)) of the material.
The heat equation can be used to model the heat flow in solids and fluids, in the latter case, however, it does not take into account the convection phenomenon; and provides a reasonable model only if phenomena such as macroscopic currents in the fluid are not present (or negligible). Further, the heat equation is not a fundamental law of physics, and it does not give reliable answers at very low or very high temperatures.
Since temperature is related to heat, which is a form of energy, the basic idea in deriving the heat equation is to use the law of conservation of energy . Below we derive the general form of the heat equation in arbitrary dimension.
1.5.2.2 Fourier's Law of Heat Conduction, Derivation of the Heat Equation
Let  be a fixed spatial domain with boundary
be a fixed spatial domain with boundary 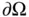 . The rate of change of thermal energy with respect to time in
. The rate of change of thermal energy with respect to time in 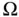 is equal to the net flow of energy across the boundary of
is equal to the net flow of energy across the boundary of 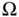 plus the rate at which heat is generated within
plus the rate at which heat is generated within 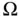 .
.
Let 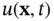 denote the temperature at the position
denote the temperature at the position 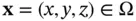 and at time
and at time 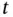 . We assume that the solid is at rest and that it is rigid, so that the only energy present is thermal energy and the density
. We assume that the solid is at rest and that it is rigid, so that the only energy present is thermal energy and the density 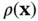 is independent of the time
is independent of the time 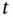 and temperature
and temperature 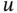 . Let
. Let 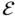 denote the energy per unit mass. Then the amount of thermal energy in
denote the energy per unit mass. Then the amount of thermal energy in 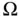 is given by
is given by
Читать дальше

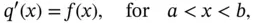
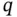 to the temperature gradient
to the temperature gradient 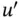 called a constitutive equation. The simplest constitutive equation for heat flow is Fourier's law :
called a constitutive equation. The simplest constitutive equation for heat flow is Fourier's law :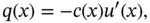
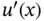 . The constant of proportionality is the coefficient of heat conductivity
. The constant of proportionality is the coefficient of heat conductivity 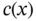 , which we assume to be a positive function in
, which we assume to be a positive function in 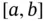 . Combining ( 1.5.4) and ( 1.5.5) gives the stationary heat equation in one dimension :
. Combining ( 1.5.4) and ( 1.5.5) gives the stationary heat equation in one dimension :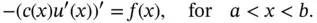
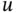 uniquely, the differential equation is complemented by boundary conditions imposed at the boundary points
uniquely, the differential equation is complemented by boundary conditions imposed at the boundary points 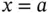 and
and 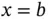 . A common example is the homogeneous Dirichlet conditions
. A common example is the homogeneous Dirichlet conditions 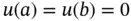 , corresponding to keeping the temperature at zero at the endpoints of the wire. The result is a two‐point BVP :
, corresponding to keeping the temperature at zero at the endpoints of the wire. The result is a two‐point BVP :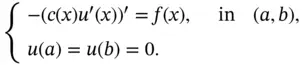
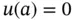 may be replaced by
may be replaced by 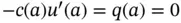 , corresponding to prescribing zero heat flux, or insulating the wire, at
, corresponding to prescribing zero heat flux, or insulating the wire, at 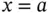 . Later, we also consider nonhomogeneous boundary conditions of the form
. Later, we also consider nonhomogeneous boundary conditions of the form 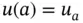 or
or 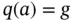 where
where 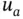 and
and 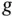 may be different from zero. For other types of boundary conditions, see Trinities ( Section 1.2).
may be different from zero. For other types of boundary conditions, see Trinities ( Section 1.2).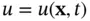 is the temperature at a position
is the temperature at a position 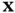 at time
at time 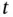 and
and 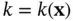 is called thermal diffusivity or heat conductivity (corresponding to
is called thermal diffusivity or heat conductivity (corresponding to 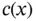 in ( 1.5.5)–( 1.5.7)) of the material.
in ( 1.5.5)–( 1.5.7)) of the material. be a fixed spatial domain with boundary
be a fixed spatial domain with boundary 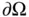 . The rate of change of thermal energy with respect to time in
. The rate of change of thermal energy with respect to time in 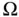 is equal to the net flow of energy across the boundary of
is equal to the net flow of energy across the boundary of 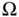 plus the rate at which heat is generated within
plus the rate at which heat is generated within 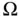 .
.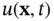 denote the temperature at the position
denote the temperature at the position 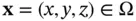 and at time
and at time 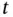 . We assume that the solid is at rest and that it is rigid, so that the only energy present is thermal energy and the density
. We assume that the solid is at rest and that it is rigid, so that the only energy present is thermal energy and the density 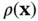 is independent of the time
is independent of the time 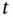 and temperature
and temperature 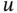 . Let
. Let 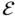 denote the energy per unit mass. Then the amount of thermal energy in
denote the energy per unit mass. Then the amount of thermal energy in 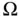 is given by
is given by










