(1.5.11) 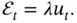
Here, 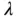 , called the specific heat , is assumed to be constant. Next, we relate the temperature
, called the specific heat , is assumed to be constant. Next, we relate the temperature 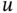 to the heat flux
to the heat flux 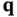 . Here, we use Fourier's law but, first, to be specific, we describe the simple facts supporting Fourier's law:
. Here, we use Fourier's law but, first, to be specific, we describe the simple facts supporting Fourier's law:
1 i. Heat flows from regions of high temperature to regions of low temperature.
2 ii. The rate of heat flux is small or large accordingly as temperature changes between neighboring regions are small or large.
To describe these quantitative properties of heat flux, we postulate a linear relationship between the rate of heat flux and the rate of temperature change. Recall that if 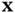 is a point in the heat‐conducting medium and
is a point in the heat‐conducting medium and 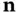 is a unit vector specifying a direction at
is a unit vector specifying a direction at 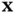 , then the rate of heat flow at
, then the rate of heat flow at 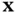 in the direction
in the direction 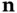 is
is 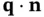 and the rate of change of the temperature is
and the rate of change of the temperature is 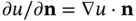 , the directional derivative of the temperature. Since
, the directional derivative of the temperature. Since 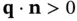 requires
requires 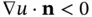 , and vice versa (from calculus the direction of maximal growth of a function is given by its gradient), our linear relation takes the form
, and vice versa (from calculus the direction of maximal growth of a function is given by its gradient), our linear relation takes the form 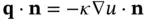 , with
, with 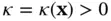 . Since
. Since 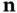 specifies any direction at
specifies any direction at 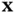 , this is equivalent to the assumption
, this is equivalent to the assumption
(1.5.12) 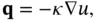
which is Fourier's law . The positive function 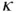 is called the heat conduction (or Fourier) coefficient . Let now
is called the heat conduction (or Fourier) coefficient . Let now 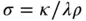 and
and 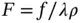 and insert ( 1.5.11) and ( 1.5.12) into ( 1.5.10) to get the final form of the heat equation:
and insert ( 1.5.11) and ( 1.5.12) into ( 1.5.10) to get the final form of the heat equation:
(1.5.13) 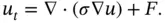
The quantity 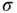 is referred to as the thermal diffusivity (or diffusion) coefficient . If we assume that
is referred to as the thermal diffusivity (or diffusion) coefficient . If we assume that 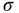 is constant, then the final form of the heat equation would be
is constant, then the final form of the heat equation would be
(1.5.14) 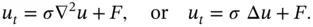
The third equation in ( 1.5.2) is the wave equation: 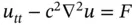 . Here,
. Here, 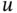 represents a wave traveling through an
represents a wave traveling through an 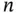 ‐dimensional medium;
‐dimensional medium; 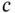 is the speed of propagation of the wave in the medium and
is the speed of propagation of the wave in the medium and 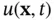 is the amplitude of the wave at position
is the amplitude of the wave at position 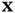 and time
and time 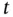 . The wave equation provides a mathematical model for a number of problems involving different physical processes as, e.g. in the following examples (i)–(vi):
. The wave equation provides a mathematical model for a number of problems involving different physical processes as, e.g. in the following examples (i)–(vi):
1 (i) Vibration of a stretched string, such as a violin string (one‐dimensional).
2 (ii)Vibration of a column of air, such as a clarinet (one‐dimensional).
3 (iii)Vibration of a stretched membrane, such as a drumhead (two‐dimensional).
4 (iv)Waves in an incompressible fluid, such as water (two‐dimensional).
5 (v)Sound waves in air or other elastic media (three‐dimensional).
6 (vi)Electromagnetic waves, such as light waves and radio waves (three‐dimensional).
Note that in (i), (iii) and (iv),  represents the transverse displacement of the string, membrane, or fluid surface; in (ii) and (v),
represents the transverse displacement of the string, membrane, or fluid surface; in (ii) and (v), 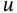 represents the longitudinal displacement of the air; and in (vi),
represents the longitudinal displacement of the air; and in (vi), 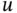 is any of the components of the electromagnetic field. For detailed discussions and a derivation of the equations modeling (i)–(vi), see, e.g. Folland [62], Strauss [129], and Taylor [134]. We should point out, however, that in most cases, the derivation involves making some simplifying assumptions. Hence, the wave equation gives only an approximate description of the actual physical process, and the validity of the approximation will depend on whether certain physical conditions are satisfied. For instance, in example (i), the vibration should be small enough so that the string is not stretched beyond its limits of elasticity. In example (vi), it follows from Maxwell's equations, the fundamental equations of electromagnetism, that the wave equation is satisfied exactly in regions containing no electrical charges or current, which of course cannot be guaranteed under normal physical circumstances and can only be approximately justified in the real world. So an attempt to derive the wave equation corresponding to each of these examples from physical principles is beyond the scope of these notes. Nevertheless, to give an idea, below we shall derive the wave equation for a vibrating string.
is any of the components of the electromagnetic field. For detailed discussions and a derivation of the equations modeling (i)–(vi), see, e.g. Folland [62], Strauss [129], and Taylor [134]. We should point out, however, that in most cases, the derivation involves making some simplifying assumptions. Hence, the wave equation gives only an approximate description of the actual physical process, and the validity of the approximation will depend on whether certain physical conditions are satisfied. For instance, in example (i), the vibration should be small enough so that the string is not stretched beyond its limits of elasticity. In example (vi), it follows from Maxwell's equations, the fundamental equations of electromagnetism, that the wave equation is satisfied exactly in regions containing no electrical charges or current, which of course cannot be guaranteed under normal physical circumstances and can only be approximately justified in the real world. So an attempt to derive the wave equation corresponding to each of these examples from physical principles is beyond the scope of these notes. Nevertheless, to give an idea, below we shall derive the wave equation for a vibrating string.
Читать дальше

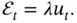
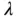 , called the specific heat , is assumed to be constant. Next, we relate the temperature
, called the specific heat , is assumed to be constant. Next, we relate the temperature 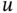 to the heat flux
to the heat flux 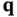 . Here, we use Fourier's law but, first, to be specific, we describe the simple facts supporting Fourier's law:
. Here, we use Fourier's law but, first, to be specific, we describe the simple facts supporting Fourier's law: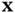 is a point in the heat‐conducting medium and
is a point in the heat‐conducting medium and 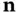 is a unit vector specifying a direction at
is a unit vector specifying a direction at 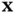 , then the rate of heat flow at
, then the rate of heat flow at 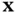 in the direction
in the direction 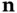 is
is 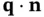 and the rate of change of the temperature is
and the rate of change of the temperature is 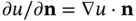 , the directional derivative of the temperature. Since
, the directional derivative of the temperature. Since 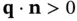 requires
requires 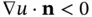 , and vice versa (from calculus the direction of maximal growth of a function is given by its gradient), our linear relation takes the form
, and vice versa (from calculus the direction of maximal growth of a function is given by its gradient), our linear relation takes the form 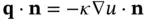 , with
, with 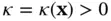 . Since
. Since 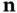 specifies any direction at
specifies any direction at 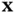 , this is equivalent to the assumption
, this is equivalent to the assumption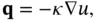
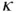 is called the heat conduction (or Fourier) coefficient . Let now
is called the heat conduction (or Fourier) coefficient . Let now 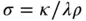 and
and 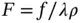 and insert ( 1.5.11) and ( 1.5.12) into ( 1.5.10) to get the final form of the heat equation:
and insert ( 1.5.11) and ( 1.5.12) into ( 1.5.10) to get the final form of the heat equation: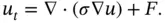
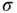 is referred to as the thermal diffusivity (or diffusion) coefficient . If we assume that
is referred to as the thermal diffusivity (or diffusion) coefficient . If we assume that 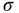 is constant, then the final form of the heat equation would be
is constant, then the final form of the heat equation would be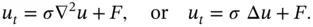
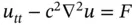 . Here,
. Here, 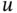 represents a wave traveling through an
represents a wave traveling through an 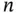 ‐dimensional medium;
‐dimensional medium; 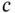 is the speed of propagation of the wave in the medium and
is the speed of propagation of the wave in the medium and 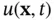 is the amplitude of the wave at position
is the amplitude of the wave at position 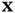 and time
and time 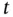 . The wave equation provides a mathematical model for a number of problems involving different physical processes as, e.g. in the following examples (i)–(vi):
. The wave equation provides a mathematical model for a number of problems involving different physical processes as, e.g. in the following examples (i)–(vi): represents the transverse displacement of the string, membrane, or fluid surface; in (ii) and (v),
represents the transverse displacement of the string, membrane, or fluid surface; in (ii) and (v), 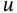 represents the longitudinal displacement of the air; and in (vi),
represents the longitudinal displacement of the air; and in (vi), 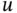 is any of the components of the electromagnetic field. For detailed discussions and a derivation of the equations modeling (i)–(vi), see, e.g. Folland [62], Strauss [129], and Taylor [134]. We should point out, however, that in most cases, the derivation involves making some simplifying assumptions. Hence, the wave equation gives only an approximate description of the actual physical process, and the validity of the approximation will depend on whether certain physical conditions are satisfied. For instance, in example (i), the vibration should be small enough so that the string is not stretched beyond its limits of elasticity. In example (vi), it follows from Maxwell's equations, the fundamental equations of electromagnetism, that the wave equation is satisfied exactly in regions containing no electrical charges or current, which of course cannot be guaranteed under normal physical circumstances and can only be approximately justified in the real world. So an attempt to derive the wave equation corresponding to each of these examples from physical principles is beyond the scope of these notes. Nevertheless, to give an idea, below we shall derive the wave equation for a vibrating string.
is any of the components of the electromagnetic field. For detailed discussions and a derivation of the equations modeling (i)–(vi), see, e.g. Folland [62], Strauss [129], and Taylor [134]. We should point out, however, that in most cases, the derivation involves making some simplifying assumptions. Hence, the wave equation gives only an approximate description of the actual physical process, and the validity of the approximation will depend on whether certain physical conditions are satisfied. For instance, in example (i), the vibration should be small enough so that the string is not stretched beyond its limits of elasticity. In example (vi), it follows from Maxwell's equations, the fundamental equations of electromagnetism, that the wave equation is satisfied exactly in regions containing no electrical charges or current, which of course cannot be guaranteed under normal physical circumstances and can only be approximately justified in the real world. So an attempt to derive the wave equation corresponding to each of these examples from physical principles is beyond the scope of these notes. Nevertheless, to give an idea, below we shall derive the wave equation for a vibrating string.










