Mohammad Asadzadeh - An Introduction to the Finite Element Method for Differential Equations

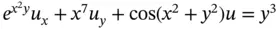Thus, for example, the equation is a linear equation, while 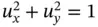is a nonlinear equation. The nonlinear equations are often further classified into subclasses according to the type of their nonlinearity. Generally, the nonlinearity is more pronounced when it appears in higher‐order derivatives. For example, the following equations are both nonlinear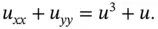

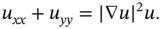
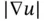(1.3.4)

(1.3.5)

Here denotes the norm of the gradient of 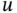. While ( 1.3.5) is nonlinear, it is still linear as a function of the highest‐order derivative (here 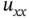and 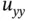). Such a nonlinearity is called quasilinear . On the other hand, in ( 1.3.4), the nonlinearity is only in the unknown solution 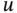. Such equations are called semilinear .

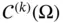Differential and integral operators are examples of mappings between function classes as where 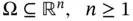. We denote by 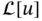the operation of a mapping (operator) 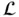on a function .

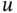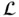An operator that satisfies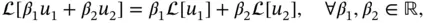

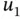(1.4.1)

where and 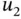are functions, is called a linear operator. We may generalize ( 1.4.1) as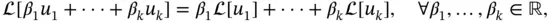

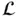(1.4.2)

i.e. maps any linear combination of 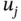's to corresponding linear combination of 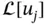's.

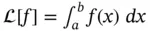For instance the integral operator defined on the space of continuous functions on 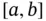defines a linear operator from 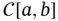into 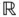, which satisfies both ( 1.4.1) and ( 1.4.2).

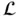A linear partial differential operator that transforms a function 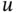of the variables into another function 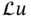is given by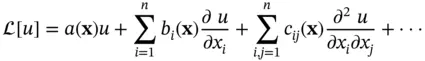

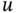(1.4.3)

where represents any function in, say 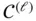, and the dots at the end indicate higher‐order derivatives, but the sums contain only finitely many terms.

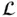The term linear in the phrase linear partial differential operator refers to the following fundamental property: if is given by ( 1.4.3) and 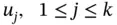, are any set of functions possessing the requisite derivatives, and 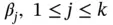are any constants, then relation ( 1.4.2) is fulfilled. This is an immediate consequence of the fact that ( 1.4.1) and ( 1.4.2) are valid for 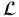replaced with the derivative of any admissible order. A linear differential equation defines a linear differential operator: the equation can be expressed as 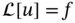, where is a linear operator and 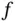is a given function. The differential equation of the form 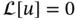is called a homogeneous equation . For example, define the operator 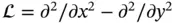. Then