As we mentioned, a key defining property of a PDE is that there are derivatives with respect to more than one independent variable and a PDE is a relation between an unknown function 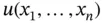 and its partial derivatives:
and its partial derivatives:
(1.3.1) 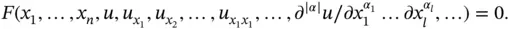
The one‐space dimensional, homogeneous, heat, and wave equations (here 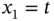 ) are among the simplest PDEs:
) are among the simplest PDEs:
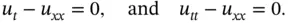
Other examples are
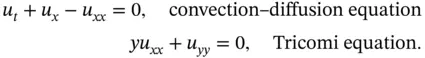
The most general PDE of first order in two independent variables, 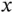 and
and 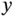 is of the form
is of the form
(1.3.2) 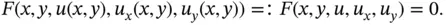
Likewise, the most general PDE of second order in two independent variables can be written as
(1.3.3) 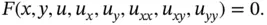
As stated in Remark 1.2, when Eqs. ( 1.3.1)–( 1.3.3) are considered in bounded domains  , in order to obtain a unique solution one should supply boundary conditions : conditions at the boundary of the domain
, in order to obtain a unique solution one should supply boundary conditions : conditions at the boundary of the domain  , denoted, e.g. by
, denoted, e.g. by 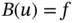 or
or 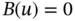 (as well as conditions for
(as well as conditions for 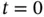 , initial conditions; denoted, e.g. by
, initial conditions; denoted, e.g. by 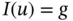 or
or 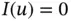 ; in the time‐dependent cases), as in the theory of ODEs.
; in the time‐dependent cases), as in the theory of ODEs. 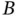 and
and  are expressions of
are expressions of 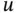 and its partial derivatives, stated on the whole or a part of the boundary of
and its partial derivatives, stated on the whole or a part of the boundary of 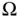 (or, in case of
(or, in case of 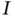 , for
, for 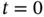 ), and are associated with the underlying PDE. Below we shall discuss the choice of relevant initial and boundary conditions for a PDE.
), and are associated with the underlying PDE. Below we shall discuss the choice of relevant initial and boundary conditions for a PDE.
A solution of a PDE of type ( 1.3.1)–( 1.3.3) is a function 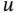 that identically satisfies the corresponding PDE, and the associated initial and boundary conditions, in some region of the variables
that identically satisfies the corresponding PDE, and the associated initial and boundary conditions, in some region of the variables 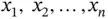 , or
, or  (and
(and 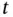 ). Note that a solution of an equation of order
). Note that a solution of an equation of order 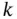 has to be
has to be 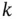 times differentiable. A function in
times differentiable. A function in 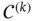 that satisfies a PDE of order
that satisfies a PDE of order 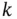 is called a classical (or strong) solution of the PDE. We sometimes also have to deal with solutions that are not classical. Such solutions are called weak solutions . In this note, in the variational formulation for FEMs, we actually deal with weak solutions. For a more thorough discussion on weak solutions, see Chapter 2 or any textbook in distribution theory.
is called a classical (or strong) solution of the PDE. We sometimes also have to deal with solutions that are not classical. Such solutions are called weak solutions . In this note, in the variational formulation for FEMs, we actually deal with weak solutions. For a more thorough discussion on weak solutions, see Chapter 2 or any textbook in distribution theory.
Definition 1.2 Hadamard's criteria; compare with the three criteria in theory
A problem consisting of a PDE associated with boundary and/or initial conditions is called well‐posed if it fulfills the following three criteria:
1 Existence The problem has a solution.
2 Uniqueness There is no more than one solution.
3 Stability A small change in the equation or in the side (initial and/or boundary) conditions gives rise to a small change in the solution.
If one or more of the conditions abovementioned does not hold, then we say that the problem is ill‐posed . The fundamental theoretical question of PDEs is whether the problem consisting of the equation and its associated side conditions is well‐posed. However, in certain engineering applications, we might encounter problems that are ill‐posed. In practice, such problems are unsolvable. Therefore, when we face an ill‐posed problem, the first step should be to modify it appropriately in order to render it well‐posed.
An equation is called linear if in ( 1.3.1), 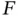 is a linear function of the unknown function
is a linear function of the unknown function 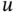 and its derivatives.
and its derivatives.
Читать дальше

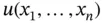 and its partial derivatives:
and its partial derivatives: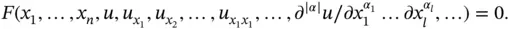
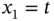 ) are among the simplest PDEs:
) are among the simplest PDEs: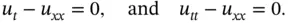
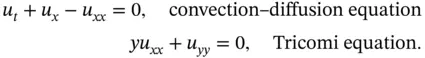
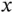 and
and 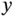 is of the form
is of the form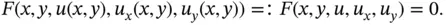
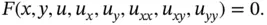
 , in order to obtain a unique solution one should supply boundary conditions : conditions at the boundary of the domain
, in order to obtain a unique solution one should supply boundary conditions : conditions at the boundary of the domain  , denoted, e.g. by
, denoted, e.g. by 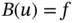 or
or 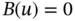 (as well as conditions for
(as well as conditions for 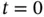 , initial conditions; denoted, e.g. by
, initial conditions; denoted, e.g. by 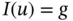 or
or 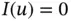 ; in the time‐dependent cases), as in the theory of ODEs.
; in the time‐dependent cases), as in the theory of ODEs. 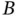 and
and 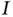 are expressions of
are expressions of 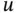 and its partial derivatives, stated on the whole or a part of the boundary of
and its partial derivatives, stated on the whole or a part of the boundary of 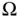 (or, in case of
(or, in case of 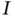 , for
, for 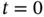 ), and are associated with the underlying PDE. Below we shall discuss the choice of relevant initial and boundary conditions for a PDE.
), and are associated with the underlying PDE. Below we shall discuss the choice of relevant initial and boundary conditions for a PDE.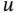 that identically satisfies the corresponding PDE, and the associated initial and boundary conditions, in some region of the variables
that identically satisfies the corresponding PDE, and the associated initial and boundary conditions, in some region of the variables 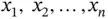 , or
, or  (and
(and 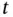 ). Note that a solution of an equation of order
). Note that a solution of an equation of order 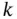 has to be
has to be 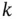 times differentiable. A function in
times differentiable. A function in 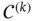 that satisfies a PDE of order
that satisfies a PDE of order 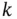 is called a classical (or strong) solution of the PDE. We sometimes also have to deal with solutions that are not classical. Such solutions are called weak solutions . In this note, in the variational formulation for FEMs, we actually deal with weak solutions. For a more thorough discussion on weak solutions, see Chapter 2 or any textbook in distribution theory.
is called a classical (or strong) solution of the PDE. We sometimes also have to deal with solutions that are not classical. Such solutions are called weak solutions . In this note, in the variational formulation for FEMs, we actually deal with weak solutions. For a more thorough discussion on weak solutions, see Chapter 2 or any textbook in distribution theory.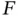 is a linear function of the unknown function
is a linear function of the unknown function 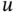 and its derivatives.
and its derivatives.










