Mohammad Asadzadeh - An Introduction to the Finite Element Method for Differential Equations

is a homogeneous equation, while the equation

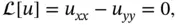
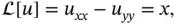
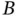is an example of an inhomogeneous equation . In a similar way, we may define another type of constraint for the PDEs that appears in many applications: the boundary conditions. In this regard, the linear boundary conditions are defined as operators satisfying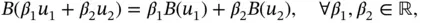

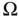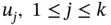(1.4.4)

at the boundary of a given domain .

Note that Laplace, heat, and wave equations are linear. Likewise, all the important boundary conditions (Dirichlet, Neumann, Robin) are linear.

The Superposition Principle.An important property of the linear operators is that if the functions , satisfy the linear differential equations 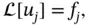and the linear boundary conditions 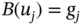for 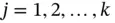, then any linear combination 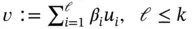, satisfies the equation 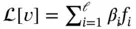as well as the boundary condition 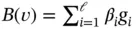. In particular, if each of the functions , satisfies the homogeneous equation 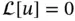and the homogeneous boundary condition 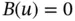, then every linear combination of them satisfies that equation and boundary condition too. This property is called the superposition principle . It allows to construct complex solutions through combining simple solutions: suppose we want to determine all solutions of a differential equation associated with a boundary condition, viz.

(1.4.5)

We consider the corresponding, simpler homogeneous problem :

(1.4.6)

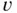Now, it suffices to find just one solution, say of the original problem ( 1.4.5). Then, for any solution of ( 1.4.5), 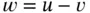satisfies ( 1.4.6), since 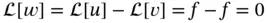and 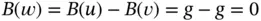. Hence, we obtain a general solution of ( 1.4.5) by adding the general (homogeneous) solution 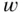of ( 1.4.6) to any particular solution of ( 1.4.5).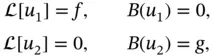

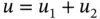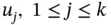Following the same idea, one may apply superposition to split a problem involving several inhomogeneous terms into simpler ones each with a single inhomogeneous term. For instance, we may split ( 1.4.5) as

and then take .

The most important application of the superposition principle is in the homogeneous case: linear homogeneous differential equations satisfying homogeneous boundary conditions (which we repeat from above).

The Superposition principle for the homogeneous case.If the functions , satisfy ( 1.4.6): the linear differential equation 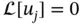and the boundary conditions (linea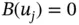r) for 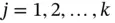, then any linear combination 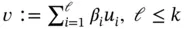, satisfies the same equation and boundary condition: ( 1.4.6).