Mohammad Asadzadeh - An Introduction to the Finite Element Method for Differential Equations
Здесь есть возможность читать онлайн «Mohammad Asadzadeh - An Introduction to the Finite Element Method for Differential Equations» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:An Introduction to the Finite Element Method for Differential Equations
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:3 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
An Introduction to the Finite Element Method for Differential Equations: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «An Introduction to the Finite Element Method for Differential Equations»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
An Introduction to the Finite Element Method (FEM) for Differential Equations
An Introduction to the Finite Element Method

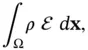
 is:
is: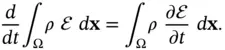
 denote the heat flux vector and
denote the heat flux vector and 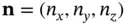 denote the outward unit normal to the boundary
denote the outward unit normal to the boundary 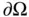 , at the point
, at the point 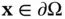 . Then
. Then 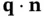 represents the flow of heat per unit cross‐sectional area per unit time crossing a surface element. Thus,
represents the flow of heat per unit cross‐sectional area per unit time crossing a surface element. Thus,
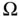 across the boundary
across the boundary 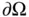 . Here,
. Here,  represents the element of surface area. The minus sign reflects the fact that if more heat flows out of the domain
represents the element of surface area. The minus sign reflects the fact that if more heat flows out of the domain 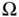 than in, the energy in
than in, the energy in  decreases. Finally, in general, the heat production is determined by external sources that are independent of the temperature. In some cases, (such as an air conditioner controlled by a thermostat), it depends on temperature itself, but not on its derivatives. Hence, in the presence of a source (or sink), we denote the corresponding rate at which heat is produced per unit volume by
decreases. Finally, in general, the heat production is determined by external sources that are independent of the temperature. In some cases, (such as an air conditioner controlled by a thermostat), it depends on temperature itself, but not on its derivatives. Hence, in the presence of a source (or sink), we denote the corresponding rate at which heat is produced per unit volume by 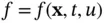 so that the source term becomes
so that the source term becomes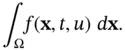
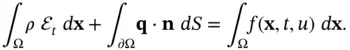
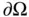 , we get
, we get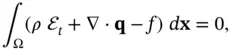
 denotes the divergence operator. In the sequel, we shall use the following simple result:
denotes the divergence operator. In the sequel, we shall use the following simple result: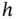 be a continuous function satisfying
be a continuous function satisfying 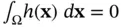 for every domain
for every domain  . Then
. Then  .
.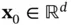 where
where  . Assume without loss of generality that
. Assume without loss of generality that 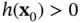 . Since
. Since  is continuous, there exists a domain (maybe very small)
is continuous, there exists a domain (maybe very small) 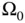 , containing
, containing  , and an
, and an 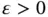 , such that
, such that  , for all
, for all 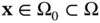 . Therefore, we have
. Therefore, we have 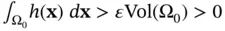 , which contradicts the assumption.
, which contradicts the assumption.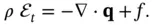
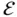 and
and 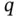 are unknown and additional information of an empirical nature is needed to determine the equation for the temperature
are unknown and additional information of an empirical nature is needed to determine the equation for the temperature  . First, for many materials, over a fairly wide but not too large temperature range, the function
. First, for many materials, over a fairly wide but not too large temperature range, the function 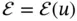 depends nearly linearly on
depends nearly linearly on 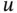 , so that
, so that










