Mohammad Asadzadeh - An Introduction to the Finite Element Method for Differential Equations
Здесь есть возможность читать онлайн «Mohammad Asadzadeh - An Introduction to the Finite Element Method for Differential Equations» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:An Introduction to the Finite Element Method for Differential Equations
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:3 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
An Introduction to the Finite Element Method for Differential Equations: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «An Introduction to the Finite Element Method for Differential Equations»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
An Introduction to the Finite Element Method (FEM) for Differential Equations
An Introduction to the Finite Element Method

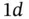
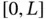 of the
of the 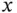 ‐axis, moving perpendicular to its equilibrium position. Let
‐axis, moving perpendicular to its equilibrium position. Let 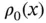 denote the density of the string in the equilibrium position and
denote the density of the string in the equilibrium position and 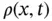 the density at time
the density at time 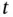 . In an arbitrary small interval
. In an arbitrary small interval 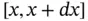 , the mass will satisfy, see Figure 1.4.
, the mass will satisfy, see Figure 1.4.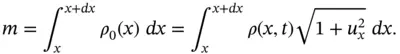
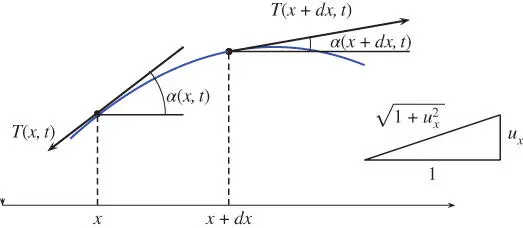
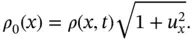
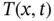 and
and 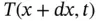 , at the endpoints of an element of the string and determine the forces acting on the small interval
, at the endpoints of an element of the string and determine the forces acting on the small interval 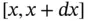 . Since we assumed that the string moves only vertically, the forces in the horizontal direction should be in balance: i.e.
. Since we assumed that the string moves only vertically, the forces in the horizontal direction should be in balance: i.e.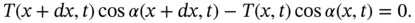
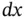 and letting
and letting 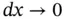 , we thus obtain
, we thus obtain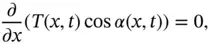
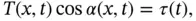
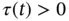 because it is the magnitude of the horizontal component of the tension.
because it is the magnitude of the horizontal component of the tension.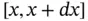 is given by
is given by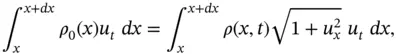
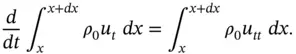
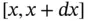 of the string: (i) the forces due to tension that keep the string taut and whose horizontal components are in balance, and (ii) the forces acting along the whole length of the string, such as weight. Thus, using ( 1.5.19), the net tension force acting on the ends of the string element
of the string: (i) the forces due to tension that keep the string taut and whose horizontal components are in balance, and (ii) the forces acting along the whole length of the string, such as weight. Thus, using ( 1.5.19), the net tension force acting on the ends of the string element 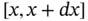 is
is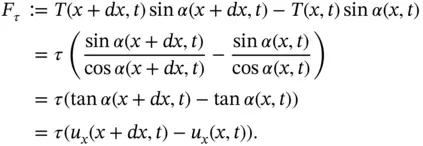
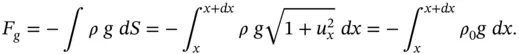
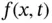 , acting on the string (e.g. when a violin string is bowed), we have
, acting on the string (e.g. when a violin string is bowed), we have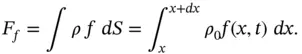
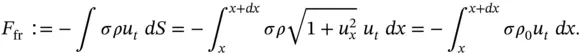
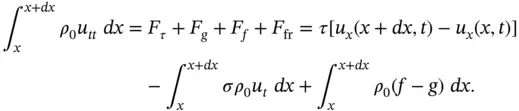
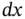 and letting
and letting 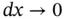 , we obtain the equation
, we obtain the equation