1 Problem 1.1 Consider the problemClearly, the function is a solution. Is this solution unique? Does the answer depend on ?
2 Problem 1.2 Consider the problemIs the solution unique? ( is a given function).Under what condition on a solution exists?
3 Problem 1.3 Suppose are solutions of the linear differential equation , where . Under what condition on the constant coefficients is the linear combination also a solution of this equation?
4 Problem 1.4 Consider the nonlinear ODE .Show that and both are solutions, but is not a solution.For which value of is a solution? What about ?
5 Problem 1.5 Show that each of the following equations has a solution of the form for a proper choice of constants . Find the constants for each example.
6 Problem 1.6Consider the equation . Write the equation in the coordinates .Find the general solution of the equation.Consider the equation . Write it in the coordinates and .
7 Problem 1.7Show that for satisfiesFind a linear combination of s that satisfies .Solve the Dirichlet problem
1.5 Some Equations of Mathematical Physics
Throughout the book, we focus on the study of some of the basic PDEs of mathematical physics. These equations involve differential operators as the gradient and Laplacian , acting on 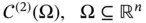 :
:
(1.5.1) 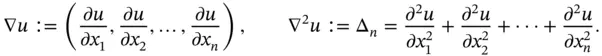
These equations describe fundamental physical phenomena as follows:
(1.5.2) 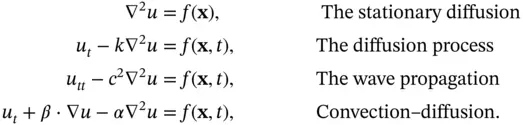
Here 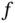 is a given function. In the special case, when
is a given function. In the special case, when  , i.e. when Eq. ( 1.5.2) are homogeneous , the first equation is called the Laplace equation and, being time‐independent, has some special features: besides the fact that it describes the steady‐state heat transfer and the standing wave equations (loosely speaking, the time‐independent versions of the other two equations), the Laplace equation arises in describing several physical phenomena such as electrostatic potential in regions with no electric charge, gravitational potential in the regions with no mass distribution, in elasticity, etc.
, i.e. when Eq. ( 1.5.2) are homogeneous , the first equation is called the Laplace equation and, being time‐independent, has some special features: besides the fact that it describes the steady‐state heat transfer and the standing wave equations (loosely speaking, the time‐independent versions of the other two equations), the Laplace equation arises in describing several physical phenomena such as electrostatic potential in regions with no electric charge, gravitational potential in the regions with no mass distribution, in elasticity, etc.
1.5.1 The Poisson Equation
The Poisson equation is a BVP of the form
(1.5.3) 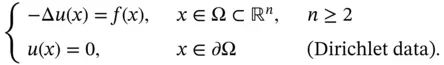
Below are some common phenomena modeled by the Poisson's equation.
Electrostatics: To describe the components of the Maxwell's equations, associating the electric‐ and potential fields and to the charge density , roughly speaking, we haveand with a Dirichlet boundary condition on .
Fluid mechanics: The velocity field of a rotation‐free fluid flow satisfies and hence, is a, so‐called, gradient field: , with being a scalar potential field. The rotation‐free incompressible fluid flow satisfies , which yields the Laplace's equation for its potential. At a solid boundary, this problem will be associated with homogeneous Neumann boundary condition, due to the fact that in such a boundary, the normal velocity is zero.
Statistical physics: The random motion of particles inside a container until they hit the boundary is described by the probability of a particle starting at the point winding up to stop at some point on , where means that it is certain and means that it never happens. It turns out that solves the Laplace's equation , with discontinuity at the boundary: on and on where . Poisson's equation is of vital importance in describing, the coupling of nonlinearity aspects, in the system of gas kinetic/dynamic equations.
1.5.2 The Heat Equation
1.5.2.1 A Model Problem for the Stationary Heat Equation in 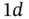
Below we model the heat conduction in a thin heat‐conducting wire stretched between the two endpoints of an interval 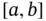 that is subject to a heat source of intensity
that is subject to a heat source of intensity 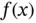 , as in Figure 1.3. We are interested in the stationary distribution of temperature
, as in Figure 1.3. We are interested in the stationary distribution of temperature 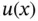 in the wire.
in the wire.
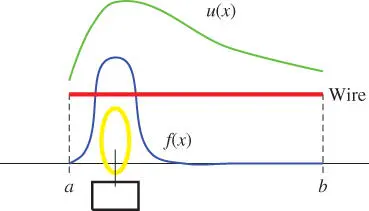
Figure 1.3A heat‐conducting one‐dimensional wire.
To this end, let 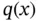 denote the heat flux in the direction of the positive
denote the heat flux in the direction of the positive 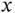 ‐axis in the wire
‐axis in the wire 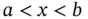 . Conservation of energy in the stationary case requires that the net heat through the endpoints of an arbitrary subinterval
. Conservation of energy in the stationary case requires that the net heat through the endpoints of an arbitrary subinterval 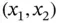 of
of 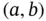 is equal to the heat produced in
is equal to the heat produced in 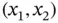 per unit time:
per unit time:
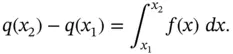
By the Fundamental Theorem of Calculus ,
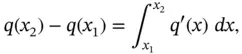
Hence, we conclude that
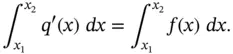
Since 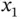 and
and 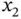 are arbitrary, assuming that the integrands are continuous, yields
are arbitrary, assuming that the integrands are continuous, yields
Читать дальше

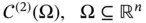 :
: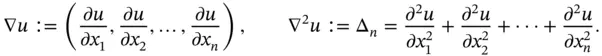
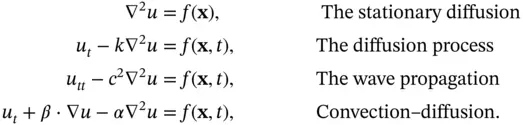
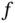 is a given function. In the special case, when
is a given function. In the special case, when  , i.e. when Eq. ( 1.5.2) are homogeneous , the first equation is called the Laplace equation and, being time‐independent, has some special features: besides the fact that it describes the steady‐state heat transfer and the standing wave equations (loosely speaking, the time‐independent versions of the other two equations), the Laplace equation arises in describing several physical phenomena such as electrostatic potential in regions with no electric charge, gravitational potential in the regions with no mass distribution, in elasticity, etc.
, i.e. when Eq. ( 1.5.2) are homogeneous , the first equation is called the Laplace equation and, being time‐independent, has some special features: besides the fact that it describes the steady‐state heat transfer and the standing wave equations (loosely speaking, the time‐independent versions of the other two equations), the Laplace equation arises in describing several physical phenomena such as electrostatic potential in regions with no electric charge, gravitational potential in the regions with no mass distribution, in elasticity, etc.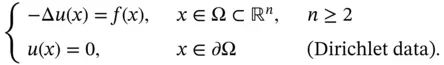
 that is subject to a heat source of intensity
that is subject to a heat source of intensity 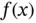 , as in Figure 1.3. We are interested in the stationary distribution of temperature
, as in Figure 1.3. We are interested in the stationary distribution of temperature 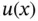 in the wire.
in the wire.
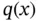 denote the heat flux in the direction of the positive
denote the heat flux in the direction of the positive 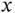 ‐axis in the wire
‐axis in the wire 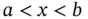 . Conservation of energy in the stationary case requires that the net heat through the endpoints of an arbitrary subinterval
. Conservation of energy in the stationary case requires that the net heat through the endpoints of an arbitrary subinterval 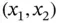 of
of 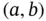 is equal to the heat produced in
is equal to the heat produced in 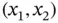 per unit time:
per unit time: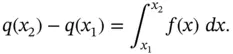
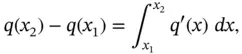
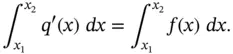
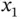 and
and 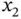 are arbitrary, assuming that the integrands are continuous, yields
are arbitrary, assuming that the integrands are continuous, yields










