Mohammad Asadzadeh - An Introduction to the Finite Element Method for Differential Equations

Editorial Office

111 River Street, Hoboken, NJ 07030, USA

For details of our global editorial offices, customer services, and more information about Wiley products visit us at www.wiley.com.

Wiley also publishes its books in a variety of electronic formats and by print‐on‐demand. Some content that appears in standard print versions of this book may not be available in other formats.

Limit of Liability/Disclaimer of Warranty

While the publisher and authors have used their best efforts in preparing this work, they make no representations or warranties with respect to the accuracy or completeness of the contents of this work and specifically disclaim all warranties, including without limitation any implied warranties of merchantability or fitness for a particular purpose. No warranty may be created or extended by sales representatives, written sales materials or promotional statements for this work. The fact that an organization, website, or product is referred to in this work as a citation and/or potential source of further information does not mean that the publisher and authors endorse the information or services the organization, website, or product may provide or recommendations it may make. This work is sold with the understanding that the publisher is not engaged in rendering professional services. The advice and strategies contained herein may not be suitable for your situation. You should consult with a specialist where appropriate. Further, readers should be aware that websites listed in this work may have changed or disappeared between when this work was written and when it is read. Neither the publisher nor authors shall be liable for any loss of profit or any other commercial damages, including but not limited to special, incidental, consequential, or other damages.

Library of Congress Cataloging‐in‐Publication Data

Names: Asadzadeh, M., author.

Title: An introduction to the finite element method for differential

equations / M. Asadzadeh.

Description: Hoboken, NJ : Wiley, [2020] | Includes bibliographical

references and index.

Identifiers: LCCN 2020008313 (print) | LCCN 2020008314 (ebook) | ISBN

9781119671640 (cloth) | ISBN 9781119671671 (adobe pdf) | ISBN

9781119671664 (epub)

Subjects: LCSH: Finite element method. | Differential equations.

Classification: LCC TA347.F5 A83 2020 (print) | LCC TA347.F5 (ebook) |

DDC 515/.35--dc23

LC record available at https://lccn.loc.gov/2020008313

LC ebook record available at https://lccn.loc.gov/2020008314

Cover Design: Wiley

Cover Image: Courtesy of: Mohammad Asadzadeh and Larisa Beilina

This book is an introduction to finite element methods (FEMs) used in the numerical solution of differential equations based on the piecewise polynomial approximations of the solutions. The presented material is accessible for upper undergraduates and starting graduate students in natural science and engineering. We mention three books for further and deeper study of FEM for differential equations.

Brenner, S.C. and Scott, L.R.The Mathematical Theory of Finite Element Methods. Springer, ed 3, 2017.

Ern, A. and Guermond, J.‐L.Theory and Practice of Finite Elements. Springer, 2004.

Larsson, S. and Thomée, V.Partial Differential Equations with Numerical Methods. Springer, 2003.

The material is presented in three main theme.

(I) Basic theory : Chapters 1and 2, contains introduction (and in some extend derivation) of basic ordinary and partial differential equations, their classifications, well‐posedness (as the proof of Reisz and Lax–Milgram Theorems) and formulation of the corresponding initial‐ and initial‐boundary value problems. The concept of fundamental solutions using Green's functions approaches are discussed and necessary mathematical tools and environment are introduced in some details.

(II) One‐space dimensional problems : Chapters 3– 7concern the polynomial approximations, polynomial interpolation, quadrature rules (numerical integration), iterative numerical methods to solve linear system of equations and finite element procedure for the one‐space dimensional boundary value problems (BVPs), initial value problems (IVPs), and initial boundary value problems (IBVPs).

(III) Problems in higher ( 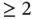) dimensional cases . This part is the matter of Chapters 8– 10and is devoted to the generalization/extension of the results of Part II to higher dimensions. The proofs in higher dimensions do not, in general, require any additional ideas. More specifically, we have introduced the higher‐dimensional interpolation procedure and study the stability and convergence aspects of certain finite element approximation for, higher‐dimensional, Poisson, heat, wave, and convection–diffusion equations. The convergence analysis are given both in the “a priori” (exact solution dependent) and “a posteriori” (computed solution/residual dependent) settings.

Whole or selected parts of the book is suitable as course material and for particular purposes. As outlined in table below, I have used some minor parts of Chapters 1and 2and the whole Chapters 3, and 5– 7, together with a theory and a computer assignment, for a 7.5 credit points for undergraduates at Chalmers University of Technology. The whole book: Chapters 1– 3(a less pronounced cover of Chapters 5– 7) together with Chapters 8– 10has been the course material for upper undergraduates and some graduates at Chalmers for more than two decades (since 1995). This part is associated with two, somewhat involved, theory and computer assignments and generates the same credit points 7.5, for a somewhat higher‐level audience. There is a, 5 credit points, intensive course on Chapters 2– 3and 8– 10for some graduates. (According to Bologna unifying system now a full‐time semester should correspond to 30 credit points.) Here, the first combination is accessible for the students with basic knowledge of calculus of single‐ and several‐variables, linear algebra and some Fourier analysis. The extended combination requires more of mathematical tools (in Chapter 2) and can be of interest for beginning graduates in applied math and engineering disciplines.

To conclude, the theory combined with approximation techniques and computer projects can give a better understanding of this useful tool (FEM) to solve differential equations. Finally, there are some easily implementable Matlab codes presented at the end of the book that are useful for freshmen in finite elements to test and check the theory through implementations.

Suggestions for possible course syllabus(what I have had)

Chapters/Sections	1 Semester	7–8 wk	Credits
1.1–1.4, 2.5, 2.6, 3, 5–7	3 h/wk	6 h/wk	5
1.1–1.4, 2.5, 2.6, 3, 5–10	4 h/wk	8 h/wk	7
except 9.2, 9.3, 10.2.3–10.2.4, 10.5.4–10.5.6
Whole material (includes Chapter 4)	6 h/wk	10 a) /wk	10

a) An intensive course for graduates in applied math/engineering.

All above configurations are associated with home and computer assignments. Examples of some assignments are given in Appendix C.