(1.96) 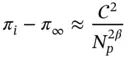
(1.97) 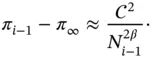
On dividing eq. (1.96)with eq. (1.97)and taking the logarithm we get
(1.98) 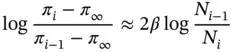
and, repeating with 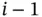 substituted for i , it is possible to eliminate
substituted for i , it is possible to eliminate 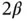 to obtain:
to obtain:
(1.99) 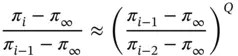
where
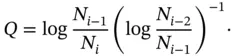
Equation (1.99)can be solved for π∞ to obtain an estimate for the exact value of the potential energy.
The relative error in energy norm corresponding to the i th finite element solution in the sequence is estimated from
(1.100) 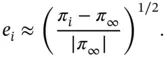
Usually the percent relative error is reported. This estimator has been tested against the known exact solution of many problems of various smoothness. The results have shown that it works well for a wide range of problems, including most problems of practical interest; however, it cannot be guaranteed to work well for all conceivable problems. For example, this method would fail if the exact solution would happen to be energy‐orthogonal to all basis functions associated with (say) odd values of i .
Remark 1.12From equation (1.92)we get
(1.101) 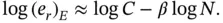
On plotting 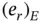 vs. N on log‐log scale a straight line with the slope
vs. N on log‐log scale a straight line with the slope 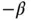 will be seen for sufficiently large N . The estimated value of β , corresponding to the i th solution in the sequence, is denoted by βi . It is computed from eq. (1.98):
will be seen for sufficiently large N . The estimated value of β , corresponding to the i th solution in the sequence, is denoted by βi . It is computed from eq. (1.98):
(1.102) 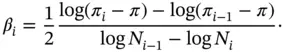
The properties of the finite element solution with reference to a family of model problems is discussed in the following. The problems are stated as follows: Find  such that
such that
(1.103) 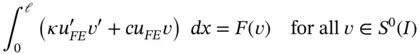
where κ and c are constants and 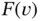 is defined such that the exact solution is:
is defined such that the exact solution is:
(1.104) 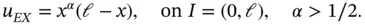
As explained in Section 1.5.1, when α is not an integer, the case considered in the following, then this solution lies in the space 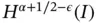 . Therefore the asymptotic rate of h ‐convergence on uniform meshes, predicted by eq. (1.92), is
. Therefore the asymptotic rate of h ‐convergence on uniform meshes, predicted by eq. (1.92), is 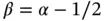 and the asymptotic rate of p ‐convergence on a fixed mesh is
and the asymptotic rate of p ‐convergence on a fixed mesh is 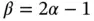 .
.
We selected this problem because it is representative of the singular part of the exact solutions of two‐and three‐dimensional elliptic boundary value problems.
Referring to Theorem 1.3, we have 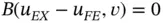 for all
for all  therefore
therefore 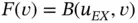 . Consequently for the k th element the load vector in the local numbering convention is:
. Consequently for the k th element the load vector in the local numbering convention is:
(1.105) 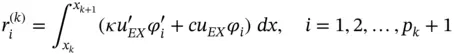
where by definition 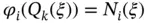 .
.
When 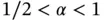 then the first derivative of
then the first derivative of 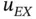 is infinity in the point
is infinity in the point 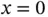 . To avoid having
. To avoid having 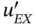 in the integrand, the first term in eq. (1.105)is integrated by parts:
in the integrand, the first term in eq. (1.105)is integrated by parts:

Since 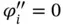 for
for 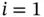 and
and 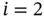 , we have:
, we have:
Читать дальше

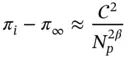
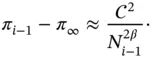
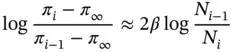
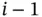 substituted for i , it is possible to eliminate
substituted for i , it is possible to eliminate 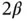 to obtain:
to obtain: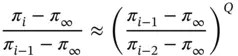
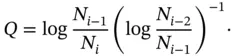
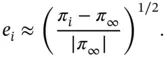
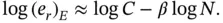
 vs. N on log‐log scale a straight line with the slope
vs. N on log‐log scale a straight line with the slope 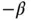 will be seen for sufficiently large N . The estimated value of β , corresponding to the i th solution in the sequence, is denoted by βi . It is computed from eq. (1.98):
will be seen for sufficiently large N . The estimated value of β , corresponding to the i th solution in the sequence, is denoted by βi . It is computed from eq. (1.98):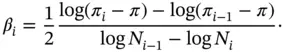
 such that
such that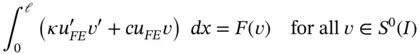
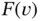 is defined such that the exact solution is:
is defined such that the exact solution is: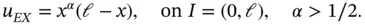
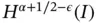 . Therefore the asymptotic rate of h ‐convergence on uniform meshes, predicted by eq. (1.92), is
. Therefore the asymptotic rate of h ‐convergence on uniform meshes, predicted by eq. (1.92), is 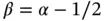 and the asymptotic rate of p ‐convergence on a fixed mesh is
and the asymptotic rate of p ‐convergence on a fixed mesh is 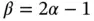 .
.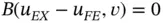 for all
for all 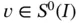 therefore
therefore 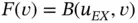 . Consequently for the k th element the load vector in the local numbering convention is:
. Consequently for the k th element the load vector in the local numbering convention is: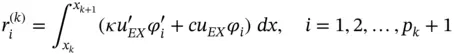
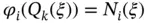 .
.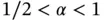 then the first derivative of
then the first derivative of 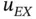 is infinity in the point
is infinity in the point 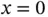 . To avoid having
. To avoid having 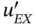 in the integrand, the first term in eq. (1.105)is integrated by parts:
in the integrand, the first term in eq. (1.105)is integrated by parts:
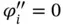 for
for  and
and  , we have:
, we have:










