which is the exact solution. The choice 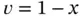 was exceptionally fortuitous because it happens to be the Green's function (also known as the influence function) for
was exceptionally fortuitous because it happens to be the Green's function (also known as the influence function) for 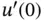 . Therefore the extracted value is independent of the solution
. Therefore the extracted value is independent of the solution 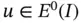 .
.
Let us choose 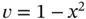 for the extraction function. In this case
for the extraction function. In this case
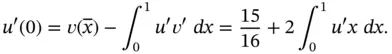
Substituting  for
for 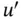 :
:
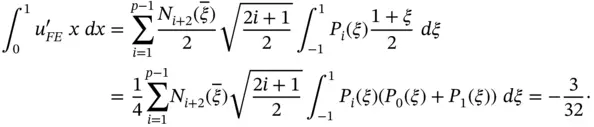
Taking the orthogonality of the Legendre polynomials (see eq. (D.13)) into account, the sum has to be evaluated only for 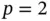 . The extracted value of
. The extracted value of 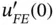 for
for 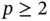 is
is 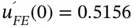 (31.25% error).
(31.25% error).
An explanation of why the extraction method is much more efficient than direct computation is given in Section 1.5.4.
Exercise 1.16Find  for the problem in Example 1.7by the direct and indirect methods. Compute the relative errors.
for the problem in Example 1.7by the direct and indirect methods. Compute the relative errors.
Exercise 1.17For the problem in Example 1.9let 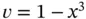 be the extraction function. Calculate the extracted value of
be the extraction function. Calculate the extracted value of 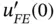 for
for 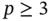 .
.
The vector of nodal forces associated with element k , denoted by 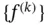 , is defined as follows:
, is defined as follows:
(1.88) 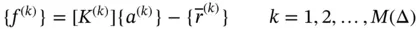
where  is the stiffness matrix,
is the stiffness matrix, 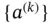 is the solution vector and
is the solution vector and 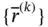 is the load vector corresponding to traction forces, concentrated forces and thermal loads acting on element k .
is the load vector corresponding to traction forces, concentrated forces and thermal loads acting on element k .
The sign convention for nodal forces is different from the sign convention for the bar force: Whereas the bar force is positive when tensile, a nodal force is positive when acting in the direction of the positive coordinate axis.
Exercise 1.18Assume that hierarchic basis functions based on Legendre polynomials are used. Show that when κ is constant and 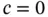 on Ik then
on Ik then
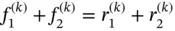
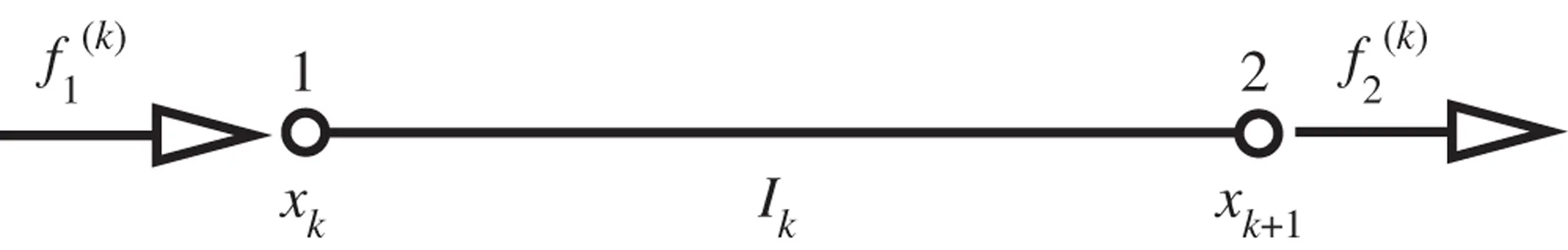
Figure 1.8 Exercise 1.18. Notation.
independently of the polynomial degree pk . For sign convention refer to Fig. 1.8. Consider both thermal and traction loads. This exercise demonstrates that nodal forces are in equilibrium independently of the finite element solution. Therefore equilibrium of nodal forces is not an indicator of the quality of finite element solutions.
1.5 Estimation of error in energy norm
We have seen that the finite element solution minimizes the error in energy norm in the sense of eq. (1.48). It is natural therefore to use the energy norm as a measure of the error of approximation. There are two types of error estimators: (a) A priori estimators that establish the asymptotic rate of convergence of a discretization scheme, given information about the regularity (smoothness) of the exact solution and (b) a posteriori estimators that provide estimates of the error in energy norm for the finite element solution of a particular problem.
There is a very substantial body of work in the mathematical literature on the a priori estimation of the rate of convergence, given a quantitative measure of the regularity of the exact solution and a sequence of discretizations. The underlying theory is outside of the scope of this book; however, understanding the main results is important for practitioners of finite element analysis. For details we refer to [28, 45, 70, 84].
Let us consider problems the exact solution of which has the functional form
(1.89) 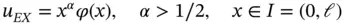
where 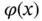 is an analytic or piecewise analytic function, see Definition A.1 in the appendix. Our motivation for considering functions in this form is that this family of functions models the singular behavior of solutions of linear elliptic boundary value problems near vertices in polygonal and polyhedral domains. For
is an analytic or piecewise analytic function, see Definition A.1 in the appendix. Our motivation for considering functions in this form is that this family of functions models the singular behavior of solutions of linear elliptic boundary value problems near vertices in polygonal and polyhedral domains. For 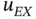 to be in the energy space, its first derivative must be square integrable on I . Therefore
to be in the energy space, its first derivative must be square integrable on I . Therefore
Читать дальше

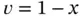 was exceptionally fortuitous because it happens to be the Green's function (also known as the influence function) for
was exceptionally fortuitous because it happens to be the Green's function (also known as the influence function) for 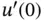 . Therefore the extracted value is independent of the solution
. Therefore the extracted value is independent of the solution 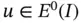 .
.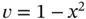 for the extraction function. In this case
for the extraction function. In this case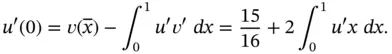
 for
for 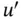 :
: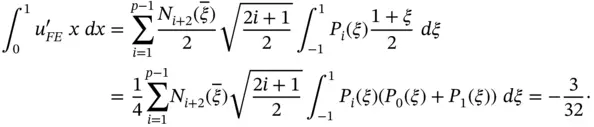
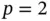 . The extracted value of
. The extracted value of 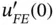 for
for 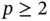 is
is 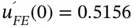 (31.25% error).
(31.25% error). for the problem in Example 1.7by the direct and indirect methods. Compute the relative errors.
for the problem in Example 1.7by the direct and indirect methods. Compute the relative errors.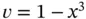 be the extraction function. Calculate the extracted value of
be the extraction function. Calculate the extracted value of 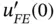 for
for 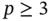 .
.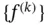 , is defined as follows:
, is defined as follows: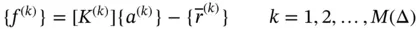
 is the stiffness matrix,
is the stiffness matrix, 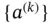 is the solution vector and
is the solution vector and 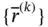 is the load vector corresponding to traction forces, concentrated forces and thermal loads acting on element k .
is the load vector corresponding to traction forces, concentrated forces and thermal loads acting on element k .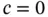 on Ik then
on Ik then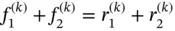
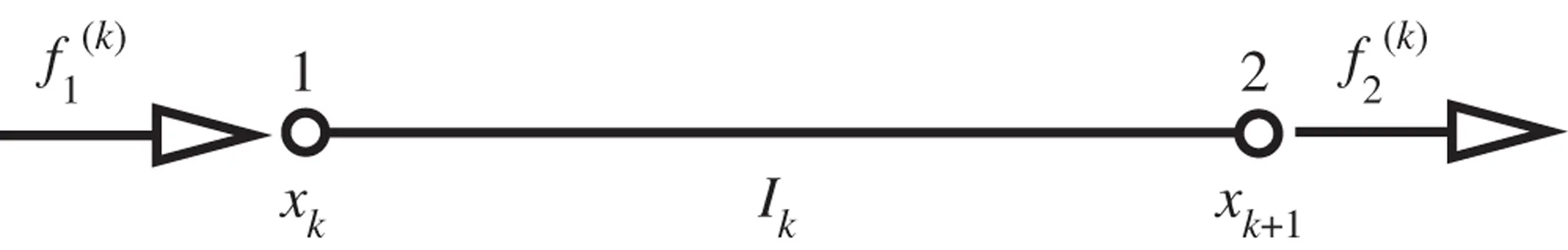
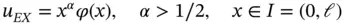
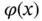 is an analytic or piecewise analytic function, see Definition A.1 in the appendix. Our motivation for considering functions in this form is that this family of functions models the singular behavior of solutions of linear elliptic boundary value problems near vertices in polygonal and polyhedral domains. For
is an analytic or piecewise analytic function, see Definition A.1 in the appendix. Our motivation for considering functions in this form is that this family of functions models the singular behavior of solutions of linear elliptic boundary value problems near vertices in polygonal and polyhedral domains. For 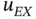 to be in the energy space, its first derivative must be square integrable on I . Therefore
to be in the energy space, its first derivative must be square integrable on I . Therefore










