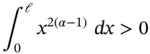
from which it follows that α must be greater than 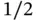 .
.
In the following we will see that when α is not an integer then the degree of difficulty associated with approximating  by the finite element method is related to the size of
by the finite element method is related to the size of  . The smaller
. The smaller 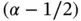 is, the more difficult it is to approximate
is, the more difficult it is to approximate 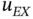 .
.
If α is a fractional number then the measure of regularity used in the mathematical literature is the maximum number of square integrable derivatives, with the notion of derivative generalized to fractional numbers. See sections A.2.3and A.2.4in the appendix. For our purposes it is sufficient to remember that if 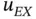 has the functional form of eq. (1.89), and α is not an integer, then
has the functional form of eq. (1.89), and α is not an integer, then 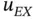 lies in the Sobolev space
lies in the Sobolev space 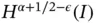 where
where 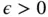 is arbitrarily small. This means that α must be larger than
is arbitrarily small. This means that α must be larger than 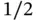 for the first derivative of
for the first derivative of 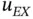 to be square integrable. See, for example, [59].
to be square integrable. See, for example, [59].
If α is an integer then 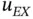 is an analytic or piecewise analytic function and the measure of regularity is the size of the derivatives of
is an analytic or piecewise analytic function and the measure of regularity is the size of the derivatives of 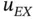 . Analogous definitions apply to two and three dimensions.
. Analogous definitions apply to two and three dimensions.
Remark 1.9The k th derivative of a function 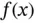 is a local property of
is a local property of 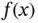 only when k is an integer. This is not the case for non‐integer derivatives.
only when k is an integer. This is not the case for non‐integer derivatives.
1.5.2 A priori estimation of the rate of convergence
Analysts are called upon to choose discretization schemes for particular problems. A sound choice of discretization is based on a priori information on the regularity of the exact solution. If we know that the exact solution lies in Sobolev space 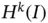 then it is possible to say how fast the error in energy norm will approach zero as the number of degrees of freedom is increased, given a scheme by which a sequence of discretizations is generated. Index k can be inferred or estimated from the input data κ , c and f .
then it is possible to say how fast the error in energy norm will approach zero as the number of degrees of freedom is increased, given a scheme by which a sequence of discretizations is generated. Index k can be inferred or estimated from the input data κ , c and f .
We define
(1.90) 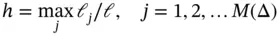
where ℓj is the length of the j th element, 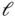 is the size of the of the solution domain
is the size of the of the solution domain 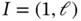 . This is generalized to two and three dimensions where
. This is generalized to two and three dimensions where 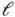 is the diameter of the domain and ℓj is the diameter of the j th element. In this context diameter means the diameter of the smallest circlein one and two dimensions, or sphere in three dimensions,that contains the element or domain. In two and three dimensions the solution domain is denoted by Ω.
is the diameter of the domain and ℓj is the diameter of the j th element. In this context diameter means the diameter of the smallest circlein one and two dimensions, or sphere in three dimensions,that contains the element or domain. In two and three dimensions the solution domain is denoted by Ω.
The a priori estimate of the relative error in energy norm for 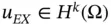 , quasiuniform meshes and polynomial degree p is
, quasiuniform meshes and polynomial degree p is
(1.91) 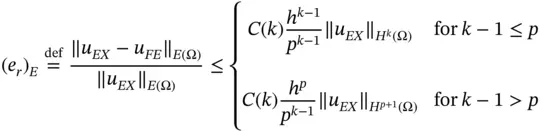
where 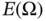 is the energy norm, k is typically a fractional number and
is the energy norm, k is typically a fractional number and 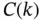 is a positive constant that depends on k but not on h or p . This inequality gives the upper bound for the asymptotic rate of convergence of the relative error in energy norm as
is a positive constant that depends on k but not on h or p . This inequality gives the upper bound for the asymptotic rate of convergence of the relative error in energy norm as 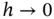 or
or 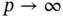 [22]. This estimate holds for one, two and three dimensions. For one and two dimensions lower bounds were proven in [13, 24] and [46] and it was shown that when singularities are located in vertex points then the rate of convergence of the p ‐version is twice the rate of convergence of the h ‐version when both are expressed in terms of the number of degrees of freedom. It is reasonable to assume that analogous results can be proven for three dimensions; however, no proofs are available at present.
[22]. This estimate holds for one, two and three dimensions. For one and two dimensions lower bounds were proven in [13, 24] and [46] and it was shown that when singularities are located in vertex points then the rate of convergence of the p ‐version is twice the rate of convergence of the h ‐version when both are expressed in terms of the number of degrees of freedom. It is reasonable to assume that analogous results can be proven for three dimensions; however, no proofs are available at present.
We will find it convenient to write the relative error in energy norm in the following form
(1.92) 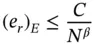
where N is the number of degrees of freedom and C and β are positive constants, β is called the algebraic rate of convergence. In one dimension 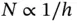 for the h ‐version and
for the h ‐version and 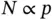 for the p ‐version. Therefore for
for the p ‐version. Therefore for 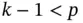 we have
we have 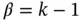 . However, for the important special case when the solution has the functional form of eq. (1.89)or, more generally, has a term like
. However, for the important special case when the solution has the functional form of eq. (1.89)or, more generally, has a term like 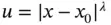 and
and 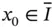 is a nodal point then
is a nodal point then 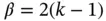 for the p ‐version: The rate of p ‐convergence is twice that of h ‐convergence [22, 84].
for the p ‐version: The rate of p ‐convergence is twice that of h ‐convergence [22, 84].
Читать дальше

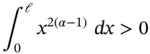
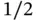 .
.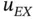 by the finite element method is related to the size of
by the finite element method is related to the size of 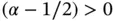 . The smaller
. The smaller 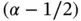 is, the more difficult it is to approximate
is, the more difficult it is to approximate 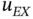 .
.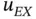 has the functional form of eq. (1.89), and α is not an integer, then
has the functional form of eq. (1.89), and α is not an integer, then 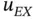 lies in the Sobolev space
lies in the Sobolev space 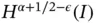 where
where 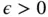 is arbitrarily small. This means that α must be larger than
is arbitrarily small. This means that α must be larger than 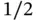 for the first derivative of
for the first derivative of 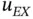 to be square integrable. See, for example, [59].
to be square integrable. See, for example, [59].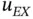 is an analytic or piecewise analytic function and the measure of regularity is the size of the derivatives of
is an analytic or piecewise analytic function and the measure of regularity is the size of the derivatives of 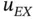 . Analogous definitions apply to two and three dimensions.
. Analogous definitions apply to two and three dimensions.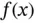 is a local property of
is a local property of 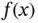 only when k is an integer. This is not the case for non‐integer derivatives.
only when k is an integer. This is not the case for non‐integer derivatives.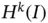 then it is possible to say how fast the error in energy norm will approach zero as the number of degrees of freedom is increased, given a scheme by which a sequence of discretizations is generated. Index k can be inferred or estimated from the input data κ , c and f .
then it is possible to say how fast the error in energy norm will approach zero as the number of degrees of freedom is increased, given a scheme by which a sequence of discretizations is generated. Index k can be inferred or estimated from the input data κ , c and f .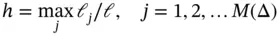
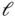 is the size of the of the solution domain
is the size of the of the solution domain 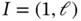 . This is generalized to two and three dimensions where
. This is generalized to two and three dimensions where 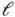 is the diameter of the domain and ℓj is the diameter of the j th element. In this context diameter means the diameter of the smallest circlein one and two dimensions, or sphere in three dimensions,that contains the element or domain. In two and three dimensions the solution domain is denoted by Ω.
is the diameter of the domain and ℓj is the diameter of the j th element. In this context diameter means the diameter of the smallest circlein one and two dimensions, or sphere in three dimensions,that contains the element or domain. In two and three dimensions the solution domain is denoted by Ω.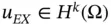 , quasiuniform meshes and polynomial degree p is
, quasiuniform meshes and polynomial degree p is
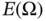 is the energy norm, k is typically a fractional number and
is the energy norm, k is typically a fractional number and 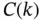 is a positive constant that depends on k but not on h or p . This inequality gives the upper bound for the asymptotic rate of convergence of the relative error in energy norm as
is a positive constant that depends on k but not on h or p . This inequality gives the upper bound for the asymptotic rate of convergence of the relative error in energy norm as 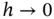 or
or 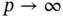 [22]. This estimate holds for one, two and three dimensions. For one and two dimensions lower bounds were proven in [13, 24] and [46] and it was shown that when singularities are located in vertex points then the rate of convergence of the p ‐version is twice the rate of convergence of the h ‐version when both are expressed in terms of the number of degrees of freedom. It is reasonable to assume that analogous results can be proven for three dimensions; however, no proofs are available at present.
[22]. This estimate holds for one, two and three dimensions. For one and two dimensions lower bounds were proven in [13, 24] and [46] and it was shown that when singularities are located in vertex points then the rate of convergence of the p ‐version is twice the rate of convergence of the h ‐version when both are expressed in terms of the number of degrees of freedom. It is reasonable to assume that analogous results can be proven for three dimensions; however, no proofs are available at present.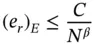
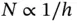 for the h ‐version and
for the h ‐version and 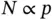 for the p ‐version. Therefore for
for the p ‐version. Therefore for 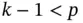 we have
we have 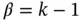 . However, for the important special case when the solution has the functional form of eq. (1.89)or, more generally, has a term like
. However, for the important special case when the solution has the functional form of eq. (1.89)or, more generally, has a term like 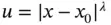 and
and 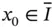 is a nodal point then
is a nodal point then 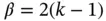 for the p ‐version: The rate of p ‐convergence is twice that of h ‐convergence [22, 84].
for the p ‐version: The rate of p ‐convergence is twice that of h ‐convergence [22, 84].










