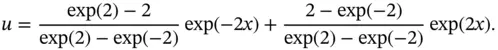
Using five elements of equal length on the interval  and
and 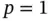 assigned to each element, find the finite element solution for this problem.
assigned to each element, find the finite element solution for this problem.
Referring to equations (1.66)and (1.70), the element‐level coefficient matrix for each element is
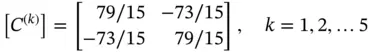
where we used 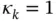 ,
, 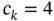 ,
, 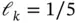 . The assembled unconstrained coefficient matrix is:
. The assembled unconstrained coefficient matrix is:

Upon enforcement of the Dirichlet conditions the system of equations is

alternatively:

where the first and sixth equations are placeholders for the boundary conditions 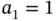 ,
, 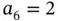 . The solution is:
. The solution is:
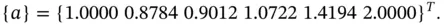
Exercise 1.14Solve the problem in Example 1.7with the boundary conditions 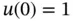 ,
, 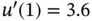 .
.
Exercise 1.15Solve the problem in Example 1.7with the boundary conditions 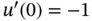 ,
, 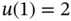 .
.
1.4 Post‐solution operations
Following assembly of the coefficient matrix and enforcement of the essential boundary conditions (when applicable) the resulting system of simultaneous equations is solved by one of several methods designed to exploit the symmetry and sparsity of the coefficient matrix. The solvers are classified into two broad categories; direct and iterative solvers. Optimal choice of a solver in a particular application is based on consideration of the size of the problem and the available computational resources.
At the end of the solution process the finite element solution is available in the form
(1.81) 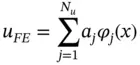
where the indices reference the global numbering and Nu is the number of degrees of freedom plus the number of Dirichlet conditions.
The basis functions are decomposed into their constituent shape functions and the element‐level solution records are created in the local numbering convention. Therefore the finite element solution on the k th element is available in the following form:
(1.82) 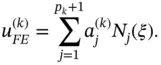
1.4.1 Computation of the quantities of interest
The computation of typical engineering quantities of interest (QoI) by direct and indirect methods is outlined in this section.
Computation of uFE ( x 0)
Direct computation of 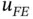 in the point
in the point 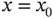 involves a search to identify the element Ik in which point x 0lies and, using the inverse of the mapping function defined by eq. (1.60), the standard coordinate
involves a search to identify the element Ik in which point x 0lies and, using the inverse of the mapping function defined by eq. (1.60), the standard coordinate 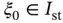 corresponding to x 0is determined:
corresponding to x 0is determined:
(1.83) 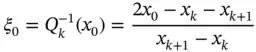
and 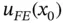 is computed from
is computed from
(1.84) 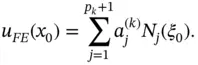
Direct computation of 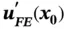
Direct computation of 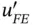 in the point x 0involves the computation of the corresponding standard coordinate
in the point x 0involves the computation of the corresponding standard coordinate 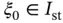 using eq. (1.83)and evaluating the following expression:
using eq. (1.83)and evaluating the following expression:
(1.85) 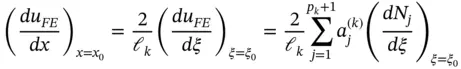
where 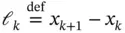 . The computation of the higher derivatives is analogous.
. The computation of the higher derivatives is analogous.
Remark 1.8When plotting quantities of interest such as the functions 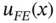 and
and 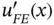 , the data for the plotting routine are generated by subdividing the standard element into n intervals of equal length, n being the desired resolution. The QoIs corresponding to the grid‐points are evaluated. This process does not involve inverse mapping. In node points information is provided from the two elements that share that node. If the computed QoI is discontinuous then the discontinuity will be visible at the nodes unless the plotting algorithm automatically averages the QoIs.
, the data for the plotting routine are generated by subdividing the standard element into n intervals of equal length, n being the desired resolution. The QoIs corresponding to the grid‐points are evaluated. This process does not involve inverse mapping. In node points information is provided from the two elements that share that node. If the computed QoI is discontinuous then the discontinuity will be visible at the nodes unless the plotting algorithm automatically averages the QoIs.
Читать дальше

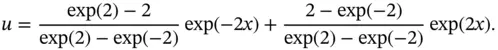
 and
and 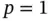 assigned to each element, find the finite element solution for this problem.
assigned to each element, find the finite element solution for this problem.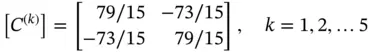
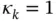 ,
, 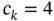 ,
, 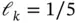 . The assembled unconstrained coefficient matrix is:
. The assembled unconstrained coefficient matrix is:


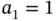 ,
, 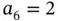 . The solution is:
. The solution is: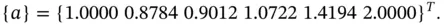
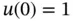 ,
, 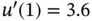 .
.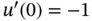 ,
, 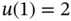 .
.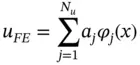
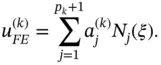
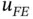 in the point
in the point 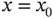 involves a search to identify the element Ik in which point x 0lies and, using the inverse of the mapping function defined by eq. (1.60), the standard coordinate
involves a search to identify the element Ik in which point x 0lies and, using the inverse of the mapping function defined by eq. (1.60), the standard coordinate 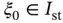 corresponding to x 0is determined:
corresponding to x 0is determined: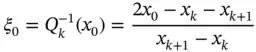
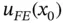 is computed from
is computed from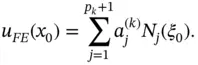
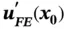
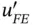 in the point x 0involves the computation of the corresponding standard coordinate
in the point x 0involves the computation of the corresponding standard coordinate 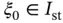 using eq. (1.83)and evaluating the following expression:
using eq. (1.83)and evaluating the following expression: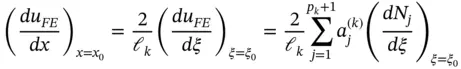
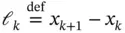 . The computation of the higher derivatives is analogous.
. The computation of the higher derivatives is analogous.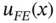 and
and 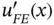 , the data for the plotting routine are generated by subdividing the standard element into n intervals of equal length, n being the desired resolution. The QoIs corresponding to the grid‐points are evaluated. This process does not involve inverse mapping. In node points information is provided from the two elements that share that node. If the computed QoI is discontinuous then the discontinuity will be visible at the nodes unless the plotting algorithm automatically averages the QoIs.
, the data for the plotting routine are generated by subdividing the standard element into n intervals of equal length, n being the desired resolution. The QoIs corresponding to the grid‐points are evaluated. This process does not involve inverse mapping. In node points information is provided from the two elements that share that node. If the computed QoI is discontinuous then the discontinuity will be visible at the nodes unless the plotting algorithm automatically averages the QoIs.










