Example 1.4When 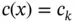 is constant on Ik and the Legendre shape functions are used then the element‐level Gram matrix is strongly diagonal. For example, for
is constant on Ik and the Legendre shape functions are used then the element‐level Gram matrix is strongly diagonal. For example, for 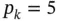 the Gram matrix is:
the Gram matrix is:
(1.70) 
Remark 1.5For 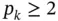 a simple closed form expression can be obtained for the diagonal terms and the off‐diagonal terms. Using eq. (1.55)it can be shown that:
a simple closed form expression can be obtained for the diagonal terms and the off‐diagonal terms. Using eq. (1.55)it can be shown that:
(1.71) 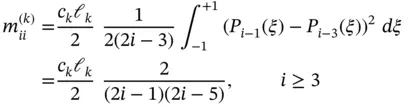
and all off‐diagonal terms are zero for 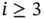 , with the exceptions:
, with the exceptions:
(1.72) 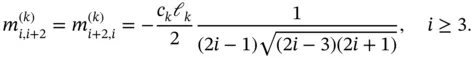
Remark 1.6It has been proposed to make the Gram matrix perfectly diagonal by using Lagrange shape functions of degree p with the node points coincident with the Lobatto points. Therefore 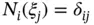 where
where 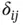 is the Kronecker delta 14 . Then, using
is the Kronecker delta 14 . Then, using 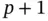 Lobatto points, we get:
Lobatto points, we get:
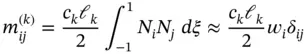
where wi is the weight of the i th Lobatto point. There is an integration error associated with this term because the integrand is a polynomial of degree 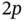 . To evaluate this integral exactly
. To evaluate this integral exactly 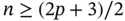 Lobatto points would be required (see Appendix E), whereas only
Lobatto points would be required (see Appendix E), whereas only 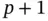 Lobatto points are used. Throughout this book we will be concerned with errors of approximation that can be controlled by the design of mesh and the assignment of polynomial degrees. We will assume that the errors of integration and errors in mapping are negligibly small in comparison with the errors of discretization.
Lobatto points are used. Throughout this book we will be concerned with errors of approximation that can be controlled by the design of mesh and the assignment of polynomial degrees. We will assume that the errors of integration and errors in mapping are negligibly small in comparison with the errors of discretization.
Exercise 1.9Assume that 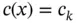 is constant on Ik . Using the Lagrange shape functions of degree
is constant on Ik . Using the Lagrange shape functions of degree 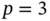 , with the nodes located in the Lobatto points, compute
, with the nodes located in the Lobatto points, compute  numerically using 4 Lobatto points. Determine the relative error of the numerically integrated term. Refer to Remark 1.6and Appendix E.
numerically using 4 Lobatto points. Determine the relative error of the numerically integrated term. Refer to Remark 1.6and Appendix E.
Exercise 1.10Assume that 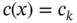 is constant on Ik . Using the Lagrange shape functions of degree
is constant on Ik . Using the Lagrange shape functions of degree 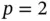 , compute
, compute 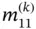 and
and 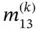 in terms of ck and ℓk .
in terms of ck and ℓk .
1.3.4 Computation of the right hand side vector
Computation of the right hand side vector involves evaluation of the functional 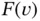 , usually by numerical means. In particular, we write:
, usually by numerical means. In particular, we write:
(1.73) 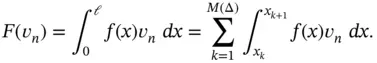
The element‐level integral is computed from the definition of vn on Ik :
(1.74) 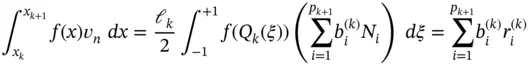
where
(1.75) 
which is computed from the given data and the shape functions.
Example 1.5Let us assume that  is a linear function on Ik . In this case
is a linear function on Ik . In this case  can be written as
can be written as
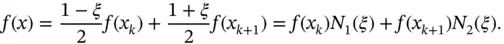
Using the Legendre shape functions we have:
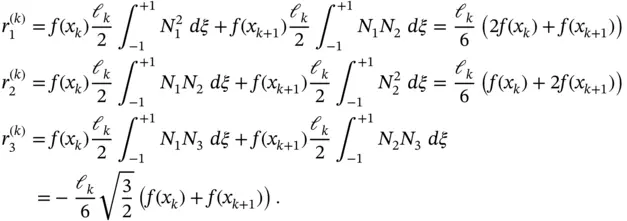
Exercise 1.11Assume that 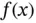 is a linear function on Ik . Using the Legendre shape functions compute
is a linear function on Ik . Using the Legendre shape functions compute 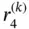 and show that
and show that 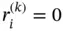 for
for 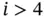 . Hint: Make use of eq. (1.55).
. Hint: Make use of eq. (1.55).
Читать дальше

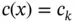 is constant on Ik and the Legendre shape functions are used then the element‐level Gram matrix is strongly diagonal. For example, for
is constant on Ik and the Legendre shape functions are used then the element‐level Gram matrix is strongly diagonal. For example, for 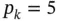 the Gram matrix is:
the Gram matrix is:
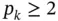 a simple closed form expression can be obtained for the diagonal terms and the off‐diagonal terms. Using eq. (1.55)it can be shown that:
a simple closed form expression can be obtained for the diagonal terms and the off‐diagonal terms. Using eq. (1.55)it can be shown that: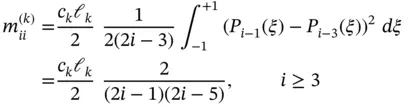
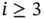 , with the exceptions:
, with the exceptions: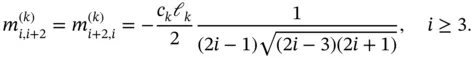
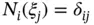 where
where 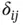 is the Kronecker delta 14 . Then, using
is the Kronecker delta 14 . Then, using 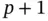 Lobatto points, we get:
Lobatto points, we get: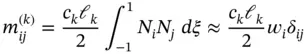
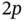 . To evaluate this integral exactly
. To evaluate this integral exactly 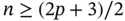 Lobatto points would be required (see Appendix E), whereas only
Lobatto points would be required (see Appendix E), whereas only 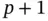 Lobatto points are used. Throughout this book we will be concerned with errors of approximation that can be controlled by the design of mesh and the assignment of polynomial degrees. We will assume that the errors of integration and errors in mapping are negligibly small in comparison with the errors of discretization.
Lobatto points are used. Throughout this book we will be concerned with errors of approximation that can be controlled by the design of mesh and the assignment of polynomial degrees. We will assume that the errors of integration and errors in mapping are negligibly small in comparison with the errors of discretization.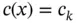 is constant on Ik . Using the Lagrange shape functions of degree
is constant on Ik . Using the Lagrange shape functions of degree 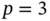 , with the nodes located in the Lobatto points, compute
, with the nodes located in the Lobatto points, compute  numerically using 4 Lobatto points. Determine the relative error of the numerically integrated term. Refer to Remark 1.6and Appendix E.
numerically using 4 Lobatto points. Determine the relative error of the numerically integrated term. Refer to Remark 1.6and Appendix E.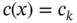 is constant on Ik . Using the Lagrange shape functions of degree
is constant on Ik . Using the Lagrange shape functions of degree 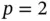 , compute
, compute 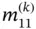 and
and 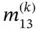 in terms of ck and ℓk .
in terms of ck and ℓk .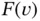 , usually by numerical means. In particular, we write:
, usually by numerical means. In particular, we write: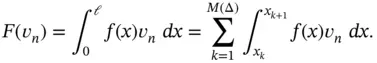
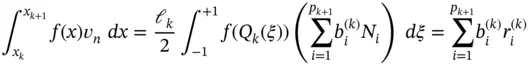

 is a linear function on Ik . In this case
is a linear function on Ik . In this case  can be written as
can be written as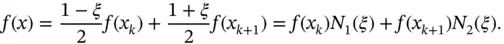
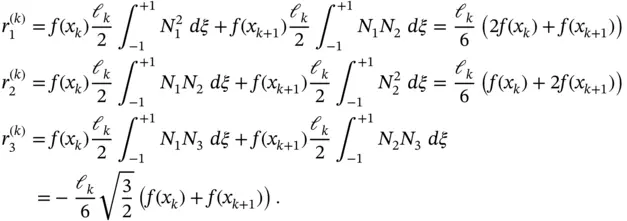
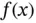 is a linear function on Ik . Using the Legendre shape functions compute
is a linear function on Ik . Using the Legendre shape functions compute 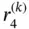 and show that
and show that 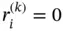 for
for 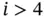 . Hint: Make use of eq. (1.55).
. Hint: Make use of eq. (1.55).










