Computation of the stiffness matrix
The first term of the bilinear form in eq. (1.43)is computed as a sum of integrals over the elements
(1.62) 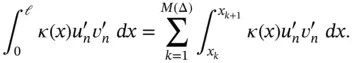
We will be concerned with the evaluation of the integral on the k th element:
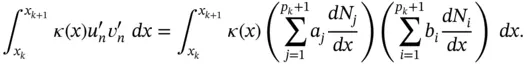
The shape functions Ni are defined on the standard domain  . Referring to the mapping function given by eq. (1.60), we have
. Referring to the mapping function given by eq. (1.60), we have
(1.63) 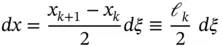
where 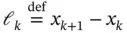 is the length of the k th element. Also,
is the length of the k th element. Also,
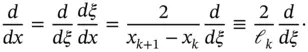
Therefore
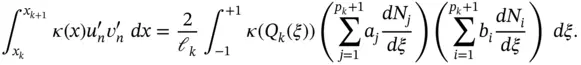
We define
(1.64) 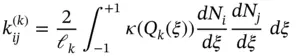
and write
(1.65) 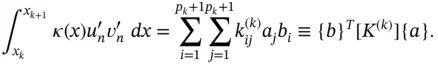
The terms of the stiffness matrix 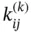 depend on the the mapping, the definition of the shape functions and the function
depend on the the mapping, the definition of the shape functions and the function 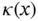 . The matrix
. The matrix 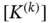 is called the element stiffness matrix. Observe that
is called the element stiffness matrix. Observe that 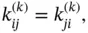 that is,
that is, 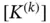 is symmetric. This follows directly from the symmetry of
is symmetric. This follows directly from the symmetry of 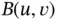 and the fact that the same basis functions are used for un and vn .
and the fact that the same basis functions are used for un and vn .
In the finite element method the integrals are evaluated by numerical methods. Numerical integration is discussed in Appendix E. In the important special case when 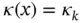 is constant on Ik , it is possible to compute
is constant on Ik , it is possible to compute 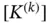 once and for all. This is illustrated by the following example.
once and for all. This is illustrated by the following example.
Example 1.3When 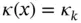 is constant on Ik and the Legendre shape functions are used then, with the exception of the first two rows and columns, the element stiffness matrix is perfectly diagonal:
is constant on Ik and the Legendre shape functions are used then, with the exception of the first two rows and columns, the element stiffness matrix is perfectly diagonal:
(1.66) 
Exercise 1.8Assume that 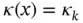 is constant on Ik . Using the Lagrange shape functions displayed in Fig. 1.3for
is constant on Ik . Using the Lagrange shape functions displayed in Fig. 1.3for 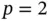 , compute
, compute 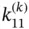 and
and 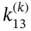 in terms of κk and ℓk .
in terms of κk and ℓk .
Computation of the Gram matrix
The second term of the bilinear form is also computed as a sum of integrals over the elements:
(1.67) 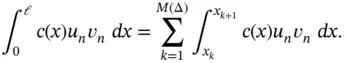
We will be concerned with evaluation of the integral
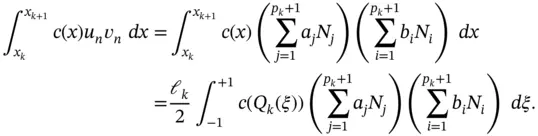
Defining:
(1.68) 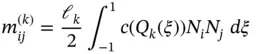
the following expression is obtained:
(1.69) 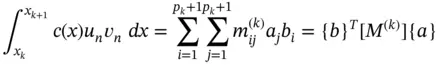
where 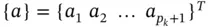 ,
, 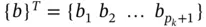 and
and
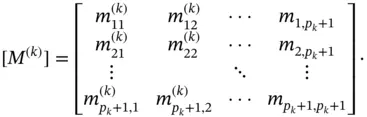
The terms of the coefficient matrix 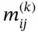 are computable from the mapping, the definition of the shape functions and the function
are computable from the mapping, the definition of the shape functions and the function 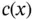 . The matrix
. The matrix 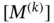 is called the element‐level Gram matrix 13 or the element‐level mass matrix. Observe that
is called the element‐level Gram matrix 13 or the element‐level mass matrix. Observe that 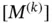 is symmetric. In the important special case where
is symmetric. In the important special case where 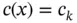 is constant on Ik it is possible to compute
is constant on Ik it is possible to compute 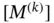 once and for all. This is illustrated by the following example.
once and for all. This is illustrated by the following example.
Читать дальше

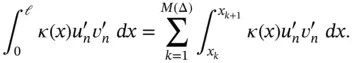
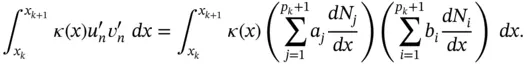
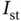 . Referring to the mapping function given by eq. (1.60), we have
. Referring to the mapping function given by eq. (1.60), we have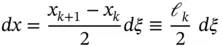
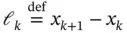 is the length of the k th element. Also,
is the length of the k th element. Also,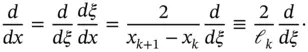
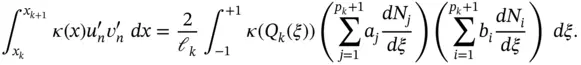
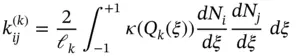
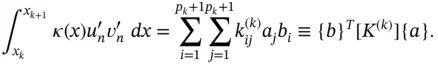
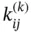 depend on the the mapping, the definition of the shape functions and the function
depend on the the mapping, the definition of the shape functions and the function 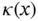 . The matrix
. The matrix 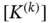 is called the element stiffness matrix. Observe that
is called the element stiffness matrix. Observe that 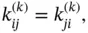 that is,
that is, 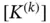 is symmetric. This follows directly from the symmetry of
is symmetric. This follows directly from the symmetry of 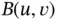 and the fact that the same basis functions are used for un and vn .
and the fact that the same basis functions are used for un and vn .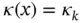 is constant on Ik , it is possible to compute
is constant on Ik , it is possible to compute 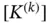 once and for all. This is illustrated by the following example.
once and for all. This is illustrated by the following example.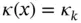 is constant on Ik and the Legendre shape functions are used then, with the exception of the first two rows and columns, the element stiffness matrix is perfectly diagonal:
is constant on Ik and the Legendre shape functions are used then, with the exception of the first two rows and columns, the element stiffness matrix is perfectly diagonal:
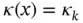 is constant on Ik . Using the Lagrange shape functions displayed in Fig. 1.3for
is constant on Ik . Using the Lagrange shape functions displayed in Fig. 1.3for 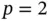 , compute
, compute 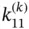 and
and 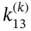 in terms of κk and ℓk .
in terms of κk and ℓk .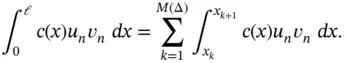
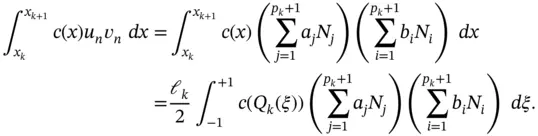
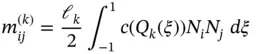
 ,
,  and
and
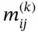 are computable from the mapping, the definition of the shape functions and the function
are computable from the mapping, the definition of the shape functions and the function 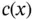 . The matrix
. The matrix 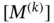 is called the element‐level Gram matrix 13 or the element‐level mass matrix. Observe that
is called the element‐level Gram matrix 13 or the element‐level mass matrix. Observe that 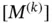 is symmetric. In the important special case where
is symmetric. In the important special case where 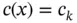 is constant on Ik it is possible to compute
is constant on Ik it is possible to compute 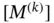 once and for all. This is illustrated by the following example.
once and for all. This is illustrated by the following example.










